This is a fixed-text formatted version of a Jupyter notebook.
You can contribute with your own notebooks in this GitHub repository.
Source files: using_numpy.ipynb | using_numpy.py
Rapid introduction on using numpy, scipy, matplotlib¶
This is meant to be a very brief reminder. It is strongly suggested to refer to more detailed introductions and tutorials see for instance: - A Whirlwind tour of Python - Python data science handbook - Scipy lectures
Introduction¶
Here we will look at : - basic features regarding array manipulation and indexing - do a bit of plotting with matplotlib - use a number of useful scipy features - see an example of vectorization with a simple Monte Carlo problem
numpy: arrays, indexing etc¶
In [1]:
import numpy as np
In [2]:
np.array([3,4,5])
Out[2]:
array([3, 4, 5])
In [3]:
np.array([[1, 2],[3,4]])
Out[3]:
array([[1, 2],
[3, 4]])
In [4]:
### linearly spaced 1D array
np.linspace(1.,10.,10)
Out[4]:
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
In [5]:
### log spaced 1D array
np.logspace(0.,1.,10)
Out[5]:
array([ 1. , 1.29154967, 1.66810054, 2.15443469,
2.7825594 , 3.59381366, 4.64158883, 5.9948425 ,
7.74263683, 10. ])
In [6]:
### 1D array of zeros
np.zeros(5)
Out[6]:
array([ 0., 0., 0., 0., 0.])
In [7]:
### 2D array of zeros
np.zeros((3,3))
Out[7]:
array([[ 0., 0., 0.],
[ 0., 0., 0.],
[ 0., 0., 0.]])
Types and casts¶
See numpy dtypes
In [8]:
x_int = np.logspace(0.,1.,10).astype('int') # cast array as int
print(x_int)
[ 1 1 1 2 2 3 4 5 7 10]
In [9]:
x_int[1] = 2.34 # 2.34 is cast as int
print(x_int[1])
2
In [10]:
array_string = np.array(['a','b','c','d'])
array_string.dtype # 1 character string
Out[10]:
dtype('<U1')
In [11]:
array_string[1]='bbbb' # 'bbbb' is cast on 1 character string
array_string[1]
Out[11]:
'b'
In [12]:
array_string = np.array(['a','b','c','d'],dtype=np.dtype('S10'))
array_string[1] = 'bbbb' # 'bbbb' is cast on 10 character string
array_string[1]
Out[12]:
b'bbbb'
array indexing & slicing¶
In [13]:
x = np.arange(10)
In [14]:
x[-1] # last element
Out[14]:
9
In [15]:
x[3:6] # subarray
Out[15]:
array([3, 4, 5])
In [16]:
x[1::2] # stride
Out[16]:
array([1, 3, 5, 7, 9])
In [17]:
x[::-1] # stride
Out[17]:
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
In [18]:
x = np.array([np.arange(10*i,10*i+5) for i in range(5)])
x
Out[18]:
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24],
[30, 31, 32, 33, 34],
[40, 41, 42, 43, 44]])
In [19]:
print("first column : ", x[:,0])
print("last row : ", x[-1,:])
first column : [ 0 10 20 30 40]
last row : [40 41 42 43 44]
In [20]:
b=x[-1,:] # This is a view not a copy!
b[:] += 1
print(x) # the initial matrix is changed!
[[ 0 1 2 3 4]
[10 11 12 13 14]
[20 21 22 23 24]
[30 31 32 33 34]
[41 42 43 44 45]]
In [21]:
# Fancy indexing
print(x % 2 == 1)
[[False True False True False]
[False True False True False]
[False True False True False]
[False True False True False]
[ True False True False True]]
In [22]:
x[x % 2 == 1] = 0
print(x)
[[ 0 0 2 0 4]
[10 0 12 0 14]
[20 0 22 0 24]
[30 0 32 0 34]
[ 0 42 0 44 0]]
Broadcasting¶
In [23]:
x = np.linspace(1, 5, 5) + 4 # 4 is broadcast to 5 element array
x
Out[23]:
array([ 5., 6., 7., 8., 9.])
In [24]:
y = np.zeros((3, 5)) + x # x is broadcast to (3,5) array
y
Out[24]:
array([[ 5., 6., 7., 8., 9.],
[ 5., 6., 7., 8., 9.],
[ 5., 6., 7., 8., 9.]])
Plotting with matplotlib¶
We will see some plotting: - Simple plots - Histograms with matplotlib
In [25]:
# This is for embedding figures in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot') # Fancy style
Vectorization or loops: A very simple MC¶
We want to solve a simple statistical question. Assume a Poisson random process of mean mu. What is the density probability function pdf(n_val) of having at least one realization of the Poisson process out of N larger than n_val?
See for instance this paper
While this problem has an analytical solution we would like to test it with a simple MC.
We will first do it as one would do it with a C code and we will progressively vectorize the problem. We will use a timer to compare performance.
In [26]:
### Define the function
def poisson_sample_maximum(mu, N, Ntrials):
"""
Generate a set of Ntrials random variables defined as the maximum of N
random Poisson R.V. of mean mu
"""
res = np.zeros(Ntrials)
### Do a loop
for i in range(Ntrials):
### Generate N random varslues
Y = np.random.poisson(mu, size=(N))
### Take the maximum
res[i] = np.max(Y)
return res
mu = 5
N = 10
Ntrials = 1000000
%timeit values = poisson_sample_maximum(mu, N, Ntrials)
1 loop, best of 3: 12.1 s per loop
It does work, but no so fast…
To do it in a efficient and pythonic way we have to avoid loops as much as possible.
The idea here will then be to do all trials at once requiring random.poisson to produce a 2D matrix of size Nxtrials
In [27]:
### Define a better function
def poisson_sample_maximum_better(mu, N, Ntrials):
"""
Generate a set of Ntrials random variables defined as the maximum of N
random Poisson R.V. of mean mu
"""
### Generate N*Ntrials random values in N x Ntrials matrix
Y = np.random.poisson(mu,size=(N,Ntrials))
### Return the maximum in each row
return np.max(Y,0)
mu = 5
N = 10
Ntrials = 1000000
%timeit values = poisson_sample_maximum_better(mu, N, Ntrials)
1 loop, best of 3: 1.1 s per loop
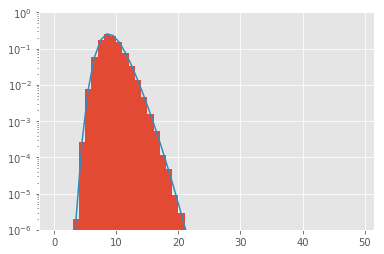
We can now compare the distribution of MC simulated values to the actual analytical function.
In [28]:
values = poisson_sample_maximum_better(mu,N,Ntrials)
### Make and plot the normalized histogram
### We define the binning ouselves to have bins for each integer
bins = np.arange(0, 10 * mu)
histo = plt.hist(values, bins=bins, normed=True, log=True)
### Now compare to the analytical solution
from scipy.special import gammaincc
### Define a lambda function to compute analytical solution
proba = lambda nv, Nr, mu_p : gammaincc(nv + 1, mu_p) ** Nr - gammaincc(nv, mu_p) ** Nr
x = 0.5 * (bins[:-1] + bins[1:])
y = proba(bins[:-1], N, mu)
plt.plot(x, y)
plt.ylim(1e-6,1) # restrict y range
Out[28]:
(1e-06, 1)
Exercices¶
- write a vectorized function that takes an array of int and returns an array where square integers are replaced by their square root and the others are left unchanged
In [29]:
### A solution
def replace_square(n):
sqrt_n = np.sqrt(n)
return n + (sqrt_n == sqrt_n.astype(int))*(-n + sqrt_n)
print(replace_square(7.0))
print(replace_square(np.arange(26)))
7.0
[ 0. 1. 2. 3. 2. 5. 6. 7. 8. 3. 10. 11. 12. 13. 14.
15. 4. 17. 18. 19. 20. 21. 22. 23. 24. 5.]
In [30]:
### or using where
def replace_square2(n):
sqrt_n = np.sqrt(n)
return np.where(sqrt_n == sqrt_n.astype(int),
sqrt_n, n)
print(replace_square2(7.0))
print(replace_square2(np.arange(26)))
7.0
[ 0. 1. 2. 3. 2. 5. 6. 7. 8. 3. 10. 11. 12. 13. 14.
15. 4. 17. 18. 19. 20. 21. 22. 23. 24. 5.]