Sphere2D

class gammapy.image.models.Sphere2D(amplitude, x_0, y_0, r_0, normed=True, **constraints)

Bases: astropy.modeling.Fittable2DModel

Projected homogeneous radiating sphere model.

This model can be used for a simple PWN source morphology.

Parameters:

amplitude : float

Value of the integral of the sphere function

x_0 : float

x position center of the sphere

y_0 : float

y position center of the sphere

r_0 : float

Radius of the sphere

normed : bool (True)

If set the amplitude parameter corresponds to the integral of the function. If not set the ‘amplitude’ parameter corresponds to the peak value of the function (value at \(r = 0\)).

See also

Shell2D, Delta2D, astropy.modeling.models.Gaussian2D

Notes

Model formula with integral normalization:

\[\begin{split}f(r) = A \frac{3}{4 \pi r_0^3} \cdot \left \{ \begin{array}{ll} \sqrt{r_0^2 - r^2} & : r \leq r_0 \\ 0 & : r > r_0 \end{array} \right.\end{split}\]

Model formula with peak normalization:

\[\begin{split}f(r) = A \frac{1}{r_0} \cdot \left \{ \begin{array}{ll} \sqrt{r_0^2 - r^2} & : r \leq r_0 \\ 0 & : r > r_0 \end{array} \right.\end{split}\]

Examples

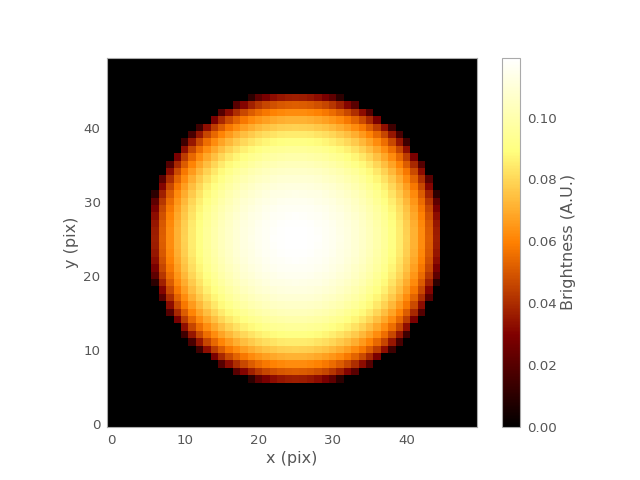
import numpy as np
import matplotlib.pyplot as plt
from gammapy.image.models import Sphere2D

sphere = Sphere2D(amplitude=100, x_0=25, y_0=25, r_0=20)
y, x = np.mgrid[0:50, 0:50]
plt.imshow(sphere(x, y), origin='lower', interpolation='none')
plt.xlabel('x (pix)')
plt.ylabel('y (pix)')
plt.colorbar(label='Brightness (A.U.)')
plt.grid(False)
plt.show()

(Source code, png, hires.png, pdf)

Attributes Summary

amplitude
param_names
r_0
x_0
y_0

Methods Summary

evaluate(x, y, amplitude, x_0, y_0, r_0)	Two dimensional Sphere model function normed to integral
evaluate_peak_norm(x, y, amplitude, x_0, ...)	Two dimensional Sphere model function normed to peak value

Attributes Documentation

amplitude

param_names = ('amplitude', 'x_0', 'y_0', 'r_0')

r_0

x_0

y_0

Methods Documentation

static evaluate(x, y, amplitude, x_0, y_0, r_0)

Two dimensional Sphere model function normed to integral

static evaluate_peak_norm(x, y, amplitude, x_0, y_0, r_0)

Two dimensional Sphere model function normed to peak value