This is a fixed-text formatted version of a Jupyter notebook

Getting started with Gammapy

Introduction

This is a getting started tutorial for Gammapy.

In this tutorial we will use the Second Fermi-LAT Catalog of High-Energy Sources (3FHL) catalog, corresponding event list and images to learn how to work with some of the central Gammapy data structures.

We will cover the following topics:

If you’re not yet familiar with the listed Astropy classes, maybe check out the Astropy introduction for Gammapy users first.

Setup

Important: to run this tutorial the environment variable GAMMAPY_DATA must be defined and point to the directory on your machine where the datasets needed are placed. To check whether your setup is correct you can execute the following cell:

[1]:

import os

path = os.path.expandvars("$GAMMAPY_DATA")

if not os.path.exists(path):
    raise Exception("gammapy-data repository not found!")
else:
    print("Great your setup is correct!")

Great your setup is correct!

In case you encounter an error, you can un-comment and execute the following cell to continue. But we recommend to set up your enviroment correctly as decribed here after you are done with this notebook.

[2]:

# os.environ['GAMMAPY_DATA'] = os.path.join(os.getcwd(), '..')

Now we can continue with the usual IPython notebooks and Python imports:

[3]:

%matplotlib inline
import matplotlib.pyplot as plt

[4]:

import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from astropy.visualization import simple_norm

Maps

The gammapy.maps package contains classes to work with sky images and cubes.

In this section, we will use a simple 2D sky image and will learn how to:

  • Read sky images from FITS files
  • Smooth images
  • Plot images
  • Cutout parts from images
  • Reproject images to different WCS
[5]:

from gammapy.maps import Map

gc_3fhl = Map.read("$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-counts.fits.gz")

The image is a WCSNDMap object:

[6]:

gc_3fhl

[6]:

WcsNDMap

    geom  : WcsGeom
    axes  : lon, lat
    shape : (400, 200)
    ndim  : 2
    unit  : ''
    dtype : >i8

The shape of the image is 400 x 200 pixel and it is defined using a cartesian projection in galactic coordinates.

The geom attribute is a WcsGeom object:

[7]:

gc_3fhl.geom

[7]:

WcsGeom

    axes       : lon, lat
    shape      : (400, 200)
    ndim       : 2
    coordsys   : GAL
    projection : CAR
    center     : 0.0 deg, 0.0 deg
    width      : 20.0 deg x 10.0 deg deg

Let’s take a closer look a the .data attribute:

[8]:

gc_3fhl.data

[8]:

array([[0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       ...,
       [0, 0, 0, ..., 0, 0, 1],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 1]])

That looks familiar! It just an ordinary 2 dimensional numpy array, which means you can apply any known numpy method to it:

[9]:

print("Total number of counts in the image: {:.0f}".format(gc_3fhl.data.sum()))

Total number of counts in the image: 32684

To show the image on the screen we can use the plot method. It basically calls plt.imshow, passing the gc_3fhl.data attribute but in addition handles axis with world coordinates using wcsaxes and defines some defaults for nicer plots (e.g. the colormap ‘afmhot’):

[10]:

gc_3fhl.plot(stretch="sqrt");
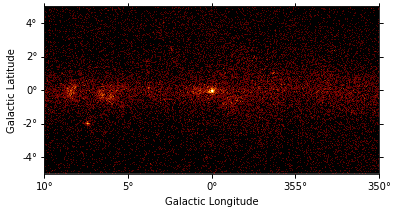
../_images/notebooks_first_steps_20_0.png

To make the structures in the image more visible we will smooth the data using a Gausian kernel with a radius of 0.5 deg. Again smooth() is a wrapper around existing functionality from the scientific Python libraries. In this case it is Scipy’s gaussian_filter method. For convenience the kernel shape can be specified with as string and the smoothing radius with a quantity. It returns again a map object, that we can plot directly the same way we did above:

[11]:

gc_3fhl_smoothed = gc_3fhl.smooth(kernel="gauss", width=0.2 * u.deg)

[12]:

gc_3fhl_smoothed.plot(stretch="sqrt");
../_images/notebooks_first_steps_23_0.png

The smoothed plot already looks much nicer, but still the image is rather large. As we are mostly interested in the inner part of the image, we will cut out a quadratic region of the size 9 deg x 9 deg around Vela. Therefore we use Map.cutout to make a cutout map:

[13]:

# define center and size of the cutout region
center = SkyCoord(0, 0, unit="deg", frame="galactic")
gc_3fhl_cutout = gc_3fhl_smoothed.cutout(center, 9 * u.deg)
gc_3fhl_cutout.plot(stretch="sqrt");
../_images/notebooks_first_steps_25_0.png

For a more detailed introdcution to ganmmapy.maps, take a look a the intro_maps.ipynb notebook.

Exercises

  • Add a marker and circle at the position of Sag A* (you can find examples in the WCSAxes documentation).
[14]:

Event lists

Almost any high-level gamma-ray data analysis starts with the raw measured counts data, which is stored in event lists. In Gammapy event lists are represented by the gammapy.data.EventList class.

In this section we will learn how to:

  • Read event lists from FITS files
  • Access and work with the EventList attributes such as .table and .energy
  • Filter events lists using convenience methods

Let’s start with the import from the gammapy.data submodule:

[14]:

from gammapy.data import EventList

Very similar to the sky map class an event list can be created, by passing a filename to the .read() method:

[15]:

events_3fhl = EventList.read(
    "$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-events.fits.gz"
)

This time the actual data is stored as an astropy.table.Table object. It can be accessed with .table attribute:

[16]:

events_3fhl.table

[16]:
Table length=32843
ENERGYRADECLBTHETAPHIZENITH_ANGLEEARTH_AZIMUTH_ANGLETIMEEVENT_IDRUN_IDRECON_VERSIONCALIB_VERSION [3]EVENT_CLASS [32]EVENT_TYPE [32]CONVERSION_TYPELIVETIMEDIFRSP0DIFRSP1DIFRSP2DIFRSP3DIFRSP4
MeVdegdegdegdegdegdegdegdegss
float32float32float32float32float32float32float32float32float32float64int32int32int16int16boolboolint16float64float32float32float32float32float32
12186.642260.45935-33.553337353.362731.753867671.977325125.5069459.22307231.79672239572401.29222104182304023957167000 .. 0False .. TrueFalse .. True0238.578372389078140.00.00.00.00.0
25496.598261.37506-34.395004353.096070.652065242.49406278.4934741.092773227.89838239577842.1621734255083323957766300 .. 0False .. TrueFalse .. False1176.168507546186450.00.00.00.00.0
15621.498259.56973-33.409416353.056732.445068464.32412234.2219466.526794232.75734239578244.7997108135317523957766300 .. 0False .. TrueFalse .. False19.3920756578445430.00.00.00.00.0
12816.32273.95883-25.3403916.45856-4.054887343.292503142.8739213.232716108.02273239605914.66160735963624123960127600 .. 0False .. TrueFalse .. False14.0347865521907810.00.00.00.00.0
18988.387260.8568-36.355804351.23734-0.10191239426.916113290.3933723.8726212.91147239611913.144604151123318823960687100 .. 0False .. TrueFalse .. True0131.601328969001770.00.00.00.00.0
11610.23266.15518-26.2244362.19860271.603481935.77363274.5338723.537594232.64166239623554.554147331415681123961832900 .. 0False .. TrueFalse .. False174.981109380722050.00.00.00.00.0
13960.802271.44742-29.6153161.6267247-4.143115525.917883238.036815.037035123.32094239634549.17487261414056923962978800 .. 0False .. TrueFalse .. False1106.373368173837660.00.00.00.00.0
10477.372266.3981-28.96814359.97003-0.01174817739.091587275.545733.02354229.59308239635161.879829821568839323962978800 .. 0False .. TrueFalse .. True0214.628174066543580.00.00.00.00.0
13030.88271.70428-20.6326279.593480.02624146852.622505161.320539.35084591.9986239639873.2076075173648223963943600 .. 0False .. TrueFalse .. True094.687530636787410.00.00.00.00.0
.....................................................................
387834.72270.3779-21.567118.1717490.6453147556.755512221.8471524.35845486.67913460185260.7970139759562646018126000 .. 0False .. TrueFalse .. True034.2146940231323240.00.00.00.00.0
20559.74268.5538-26.3456923.200638-0.3032898649.523575233.6728512.370642250.35716460185803.2027966878559046018126000 .. 0False .. TrueFalse .. True0103.176299691200260.00.00.00.00.0
27209.146266.59344-30.52607358.72775-0.9671817462.1856140.2743432.686306109.74662460190778.6372646727445346018697600 .. 0False .. TrueFalse .. True043.223347127437590.00.00.00.00.0
13911.061269.30997-27.2394392.7684028-1.336530165.15399224.5210153.017742242.62904460197889.26526911204988746019219800 .. 0False .. TrueFalse .. True095.463564038276670.00.00.00.00.0
13226.425265.16287-27.3442380.77969421.768017859.38332126.701932.12299246.97205460203215.108161451171688846019823500 .. 0False .. TrueFalse .. False13.7330975532531740.00.00.00.00.0
17445.463266.63342-28.8072010.21464892-0.103970555.48627135.5915514.227151106.7812460225372.9842249167908246022493300 .. 0False .. TrueFalse .. False180.522352814674380.00.00.00.00.0
13133.864270.42474-22.6510587.2511850.07135820448.704975134.731022.489122294.48605460225688.52486295287933546022493300 .. 0False .. TrueFalse .. False1117.881733417510990.00.00.00.00.0
32095.705266.0002-29.77206359.1034-0.1361523145.013103236.724986.92107212.86594460231367.1387127111370646023108400 .. 0False .. TrueFalse .. True0108.929764926433560.00.00.00.00.0
18465.783266.39728-29.105953359.85202-0.0829405855.97552135.8778718.909636112.137924459939497.057684768983145993557200 .. 0False .. TrueFalse .. True070.726386845111850.00.00.00.00.0
14457.25262.72217-34.388405353.7184-0.2690681245.683174237.7416225.728264240.87035459945845.47984051004968045994130200 .. 0False .. TrueFalse .. True0147.42747879028320.00.00.00.00.0

You can do len over event_3fhl.table to find the total number of events.

[17]:

print("Total number of events: {}".format(len(events_3fhl.table)))

Total number of events: 32843

And we can access any other attribute of the Table object as well:

[18]:

events_3fhl.table.colnames

[18]:

['ENERGY',
 'RA',
 'DEC',
 'L',
 'B',
 'THETA',
 'PHI',
 'ZENITH_ANGLE',
 'EARTH_AZIMUTH_ANGLE',
 'TIME',
 'EVENT_ID',
 'RUN_ID',
 'RECON_VERSION',
 'CALIB_VERSION',
 'EVENT_CLASS',
 'EVENT_TYPE',
 'CONVERSION_TYPE',
 'LIVETIME',
 'DIFRSP0',
 'DIFRSP1',
 'DIFRSP2',
 'DIFRSP3',
 'DIFRSP4']

For convenience we can access the most important event parameters as properties on the EventList objects. The attributes will return corresponding Astropy objects to represent the data, such as astropy.units.Quantity, astropy.coordinates.SkyCoord or astropy.time.Time objects:

[19]:

events_3fhl.energy.to("GeV")

[19]:
$$[12.186643,~25.496599,~15.621499,~\dots,~32.095707,~18.465784,~14.457251] \; \mathrm{GeV}$$
[20]:

events_3fhl.galactic
# events_3fhl.radec

[20]:

<SkyCoord (Galactic): (l, b) in deg
    [(353.36228879,  1.75408483), (353.09562941,  0.6522806 ),
     (353.05628243,  2.44528685), ..., (359.10295505, -0.1359316 ),
     (359.85157506, -0.08269984), (353.71795506, -0.26883694)]>

[21]:

events_3fhl.time

[21]:

<Time object: scale='tt' format='mjd' value=[54682.82946153 54682.89243456 54682.89709472 ... 57236.75267735
 57233.37455141 57233.44802852]>

In addition EventList provides convenience methods to filter the event lists. One possible use case is to find the highest energy event within a radius of 0.5 deg around the vela position:

[22]:

# select all events within a radius of 0.5 deg around center
events_gc_3fhl = events_3fhl.select_sky_cone(center=center, radius=0.5 * u.deg)

# sort events by energy
events_gc_3fhl.table.sort("ENERGY")

# and show highest energy photon
events_gc_3fhl.energy[-1].to("GeV")

[22]:
$$1917.8592 \; \mathrm{GeV}$$

Exercises

  • Make a counts energy spectrum for the galactic center region, within a radius of 10 deg.
[23]:

Source catalogs

Gammapy provides a convenient interface to access and work with catalog based data.

In this section we will learn how to:

  • Load builtins catalogs from gammapy.catalog
  • Sort and index the underlying Astropy tables
  • Access data from individual sources

Let’s start with importing the 3FHL catalog object from the gammapy.catalog submodule:

[23]:

from gammapy.catalog import SourceCatalog3FHL

First we initialize the Fermi-LAT 3FHL catalog and directly take a look at the .table attribute:

[24]:

fermi_3fhl = SourceCatalog3FHL()
fermi_3fhl.table

[24]:
Table masked=True length=1556
Source_NameRAJ2000DEJ2000GLONGLATConf_95_SemiMajorConf_95_SemiMinorConf_95_PosAngROI_numSignif_AvgPivot_EnergyFlux_DensityUnc_Flux_DensityFluxUnc_FluxEnergy_FluxUnc_Energy_FluxSignif_CurveSpectrumTypeSpectral_IndexUnc_Spectral_IndexbetaUnc_betaPowerLaw_IndexUnc_PowerLaw_IndexFlux_Band [5]Unc_Flux_Band [5,2]nuFnu [5]Sqrt_TS_Band [5]NpredHEP_EnergyHEP_ProbVariability_BayesBlocksExtended_Source_NameASSOC_GAMTEVCAT_FLAGASSOC_TEVCLASSASSOC1ASSOC2ASSOC_PROB_BAYASSOC_PROB_LRRedshiftNuPeak_obs
degdegdegdegdegdegdegGeV1 / (cm2 GeV s)1 / (cm2 GeV s)1 / (cm2 s)1 / (cm2 s)erg / (cm2 s)erg / (cm2 s)1 / (cm2 s)1 / (cm2 s)erg / (cm2 s)GeVHz
bytes18float32float32float32float32float32float32float32int16float32float32float32float32float32float32float32float32float32bytes11float32float32float32float32float32float32float32float32float32float32float32float32float32int16bytes18bytes18bytes1bytes21bytes7bytes26bytes26float32float32float32float32
3FHL J0001.2-07480.3107-7.807589.0094-67.31180.04240.0424nan645.36223.735.3174e-132.0975e-132.9593e-111.1704e-111.6752e-121.0743e-121.02PowerLaw1.67240.82740.59160.71292.22260.48081.1127661e-11 .. 1.1422301e-22-6.0763976e-12 .. 6.529277e-123.533989e-13 .. 1.1789072e-223.1458344 .. 0.07.6386.9750.996413FGL J0001.2-0748NbllPMN J0001-07460.99740.9721nan306196370000000.0
3FHL J0001.9-41550.4849-41.9303334.1216-72.06970.10180.1018nan4295.63828.425.4253e-131.6839e-134.3230e-111.3428e-113.4900e-121.8276e-120.45PowerLaw1.78190.49410.11870.27981.94180.31002.1003905e-11 .. 1.9287885e-18-8.032091e-12 .. 5.8594097e-126.7452245e-13 .. 2.078675e-184.899907 .. 0.012.51266.6250.962213FGL J0002.2-4152Nbcu1RXS J000135.5-4155190.99600.0000nan6309576500000000.0
3FHL J0002.1-67280.5283-67.4825310.0868-48.95490.03570.0357nan3868.47020.821.2062e-123.2106e-135.0093e-111.3349e-112.3058e-129.5580e-131.53PowerLaw1.81090.62600.79330.59562.42850.37102.4550664e-11 .. 1.9009976e-21-8.634195e-12 .. 4.8021903e-127.7340695e-13 .. 1.9026535e-215.900217 .. 0.017.1152.1520.998813FGL J0002.0-6722NbcuSUMSS J000215-6726530.00000.9395nan4466832000000000.0
3FHL J0003.3-52480.8300-52.8150318.9245-62.79360.04250.0425nan1457.22923.667.5065e-132.3102e-134.1560e-111.2839e-112.2874e-121.1145e-121.70PowerLaw1.60100.56440.99720.17212.24810.37322.0886386e-11 .. 7.5867555e-23-8.143967e-12 .. 5.31299e-126.6265456e-13 .. 7.800202e-235.298393 .. 0.013.0267.3100.963613FGL J0003.2-5246NbcuRBS 00060.99960.9716nan7.079464e+16
3FHL J0007.0+73031.764773.0560119.662510.46660.01010.0101nan27775.26512.801.7436e-107.5950e-121.5308e-096.1341e-113.6785e-111.5973e-123.24LogParabola3.17510.21030.90210.26593.83150.11411.3514667e-09 .. 3.839895e-18-5.7581186e-11 .. 4.060418e-124.109739e-11 .. 2.9231144e-1871.33829 .. 0.0654.1560.2920.997213FGL J0007.0+7302ECTA 1PSRLAT PSR J0007+73031.00000.0000nannan
3FHL J0007.9+47111.993147.1920115.3093-15.03540.01960.0196nan30217.77417.195.9778e-128.7683e-131.5131e-102.2181e-115.1444e-121.0540e-120.56PowerLaw2.67830.41960.16960.32822.85880.26851.0582407e-10 .. 1.9819723e-16-1.7538379e-11 .. 4.823511e-123.278615e-12 .. 1.8668298e-1615.209969 .. 0.050.9568.1520.975913FGL J0008.0+4713NbllMG4 J000800+47121.00000.98730.28002511884200000000.0
3FHL J0008.4-23392.1243-23.651450.2908-79.70210.03660.0366nan5179.67916.963.0610e-127.3475e-137.4602e-111.7896e-112.4733e-128.1716e-130.34PowerLaw2.73880.71450.17370.56182.90700.45205.804992e-11 .. 1.1117311e-20-1.4419374e-11 .. 6.10661e-121.7951775e-12 .. 1.0403958e-209.133706 .. 0.019.8371.1220.996813FGL J0008.6-2340NbllRBS 00160.99960.96730.1470524807800000000.0
3FHL J0009.1+06282.28746.4814104.4637-54.86690.03850.0385nan4026.28218.921.2691e-124.3696e-134.1597e-111.4317e-111.6903e-128.9372e-130.10PowerLaw2.55290.83630.01220.44772.58000.53912.4161059e-11 .. 6.6482124e-19-9.546595e-12 .. 6.287476e-127.566492e-13 .. 6.5095056e-194.678369 .. 0.010.9512.2560.972113FGL J0009.1+0630NbllCRATES J000903.95+062821.50.99930.9878nan663742400000000.0
3FHL J0009.4+50302.350450.5049116.1257-11.81050.01760.0176nan30222.40217.049.8252e-121.3192e-122.2191e-102.6212e-118.7336e-121.2488e-123.15LogParabola1.43050.35050.79650.30722.36100.16111.16274e-10 .. 9.252794e-17-1.8225135e-11 .. 4.417993e-123.8564165e-12 .. 7.0436765e-1715.780677 .. 0.078.5072.7620.995023FGL J0009.3+5030CbllNVSS J000922+5030281.00000.9698nan1412536400000000.0
....................................................................................................................................
3FHL J2347.9-1630356.9978-16.510665.5355-71.87660.02880.0288nan4509.29716.283.1279e-128.0896e-136.7585e-111.7478e-112.0267e-126.5608e-130.07PowerLaw3.12590.77810.01040.57563.13240.52595.2519888e-11 .. 1.0747592e-20-1.4230782e-11 .. 6.211813e-121.6103665e-12 .. 9.768252e-218.333468 .. 0.017.5550.2150.986933FGL J2348.0-1630NfsrqPKS 2345-160.99940.99990.57609332549000000.0
3FHL J2350.5-3006357.6354-30.107016.7759-76.31940.04910.0491nan706.49721.201.0879e-123.2997e-134.7039e-111.4274e-112.2909e-121.1390e-120.63PowerLaw2.10120.61730.28800.48702.36780.42342.1939225e-11 .. 4.5892933e-16-8.926376e-12 .. 6.097474e-126.927891e-13 .. 4.63469e-164.0536985 .. 0.012.8449.2860.964413FGL J2350.4-3004NbllNVSS J235034-3006030.99980.92180.22373981075200000000.0
3FHL J2351.5-7559357.8926-75.9890307.6546-40.58550.06500.0650nan556.06726.824.9826e-131.6350e-133.5689e-111.1769e-112.3897e-121.2622e-120.61PowerLaw1.84740.58020.20030.36612.08160.35322.3730832e-11 .. 6.9375605e-17-8.570627e-12 .. 4.7928705e-127.578736e-13 .. 7.316245e-175.2754674 .. 0.012.41134.7210.989213FGL J2351.9-7601NbllSUMSS J235115-7600120.00000.9625nannan
3FHL J2352.1+1753358.041517.8865103.5764-42.74660.08380.0838nan1854.11716.979.9227e-134.3475e-132.4254e-111.0640e-117.6327e-134.2356e-130.02PowerLaw3.01751.21640.01000.85243.01660.82701.5997077e-11 .. 2.9107688e-20-7.581037e-12 .. 5.821708e-124.926488e-13 .. 2.6849966e-203.5496242 .. 0.06.7343.1070.966813FGL J2352.0+1752NbllCLASS J2352+17490.99260.0000nan1737799900000000.0
3FHL J2356.2+4035359.074640.5985111.7521-21.07320.02980.0298nan3127.62529.015.2427e-131.5104e-134.3400e-111.2511e-113.6677e-121.8547e-120.35PowerLaw2.02330.4242-0.07060.19261.90950.29752.5777725e-11 .. 3.110794e-16-8.514681e-12 .. 5.4134618e-128.2889175e-13 .. 3.3694582e-166.2127647 .. 0.013.81417.8610.911913FGL J2356.0+4037NbllNVSS J235612+4036480.99980.91990.13106309576500000000.0
3FHL J2357.4-1717359.3690-17.299668.4009-74.12850.03270.0327nan4506.96129.525.4394e-131.7370e-134.6654e-111.4945e-113.7598e-121.9583e-121.11PowerLaw1.57620.51870.35130.37711.94300.31161.9003682e-11 .. 2.714288e-20-8.131149e-12 .. 6.4742196e-126.1025685e-13 .. 2.92465e-204.552822 .. 0.012.30146.7570.983813FGL J2357.4-1716NbllRBS 20660.99990.9631nan8.912525e+16
3FHL J2358.4-1808359.6205-18.140866.5520-74.85010.05110.0511nan4506.49318.231.6335e-124.9686e-134.8680e-111.4811e-111.7825e-127.6480e-131.83PowerLaw2.05320.66730.99990.01342.73120.50242.6735683e-11 .. 6.0349635e-21-9.960717e-12 .. 6.2551535e-128.323882e-13 .. 5.7844478e-214.3616037 .. 0.012.7428.3040.984513FGL J2358.6-1809N0.00000.0000nannan
3FHL J2358.5+3829359.626638.4963111.6905-23.21730.05840.0584nan3125.79718.241.4104e-124.4534e-134.2106e-111.3321e-111.7404e-129.8271e-130.44PowerLaw2.74660.6917-0.13290.30132.55760.57812.824428e-11 .. 9.750687e-17-9.458818e-12 .. 5.2791343e-128.852925e-13 .. 9.5778846e-175.7128677 .. 0.013.1357.3010.978213FGL J2358.5+3827NbcuB3 2355+3820.00000.9254nannan
3FHL J2359.1-3038359.7760-30.639712.7909-78.02680.02310.0231nan7011.55121.211.8903e-124.1965e-138.1774e-111.8149e-114.2849e-121.6806e-120.08PowerLaw2.28650.46320.01010.24342.29440.30925.5015617e-11 .. 6.037456e-17-1.3604539e-11 .. 8.488618e-121.7422797e-12 .. 6.164239e-179.39347 .. 0.022.41111.3660.960713FGL J2359.3-3038PH 2356-309bllH 2356-3090.99990.99750.16502.818388e+17
3FHL J2359.3-2049359.8293-20.825658.0522-76.54110.07220.0722nan5804.63819.029.1911e-133.6043e-133.0559e-111.1979e-111.2593e-127.4704e-130.32PowerLaw2.34020.94450.18510.66002.56150.58382.3253791e-11 .. 8.3778735e-21-8.939083e-12 .. 6.2386546e-127.2875863e-13 .. 8.224765e-214.8207045 .. 0.08.0664.1770.985913FGL J2359.5-2052NbllTXS 2356-2100.98940.99060.09604073799600000000.0

This looks very familiar again. The data is just stored as an astropy.table.Table object. We have all the methods and attributes of the Table object available. E.g. we can sort the underlying table by Signif_Avg to find the top 5 most significant sources:

[25]:

# sort table by significance
fermi_3fhl.table.sort("Signif_Avg")

# invert the order to find the highest values and take the top 5
top_five_TS_3fhl = fermi_3fhl.table[::-1][:5]

# print the top five significant sources with association and source class
top_five_TS_3fhl[["Source_Name", "ASSOC1", "ASSOC2", "CLASS", "Signif_Avg"]]

[25]:
Table masked=True length=5
Source_NameASSOC1ASSOC2CLASSSignif_Avg
bytes18bytes26bytes26bytes7float32
3FHL J0534.5+2201Crab NebulaPWN168.641
3FHL J1104.4+3812Mkn 421BLL144.406
3FHL J0835.3-4510PSR J0835-4510Vela X fieldPSR138.801
3FHL J0633.9+1746PSR J0633+1746PSR99.734
3FHL J1555.7+1111PG 1553+113BLL94.411

If you are interested in the data of an individual source you can access the information from catalog using the name of the source or any alias source name that is defined in the catalog:

[26]:

mkn_421_3fhl = fermi_3fhl["3FHL J1104.4+3812"]

# or use any alias source name that is defined in the catalog
mkn_421_3fhl = fermi_3fhl["Mkn 421"]
print(mkn_421_3fhl.data["Signif_Avg"])

144.40611

Exercises

[27]:

Spectral models and flux points

In the previous section we learned how access basic data from individual sources in the catalog. Now we will go one step further and explore the full spectral information of sources. We will learn how to:

  • Plot spectral models
  • Compute integral and energy fluxes
  • Read and plot flux points

As a first example we will start with the Crab Nebula:

[27]:

crab_3fhl = fermi_3fhl["Crab Nebula"]
print(crab_3fhl.spectral_model)

PowerLaw

Parameters:

           name     value     error        unit      min max frozen
        --------- --------- --------- -------------- --- --- ------
            index 2.220e+00 2.498e-02                nan nan  False
        amplitude 1.713e-10 3.389e-12 cm-2 GeV-1 s-1 nan nan  False
        reference 2.273e+01 0.000e+00            GeV nan nan   True

Covariance:

           name     index   amplitude reference
        --------- --------- --------- ---------
            index 6.241e-04 0.000e+00 0.000e+00
        amplitude 0.000e+00 1.148e-23 0.000e+00
        reference 0.000e+00 0.000e+00 0.000e+00

The crab_3fhl.spectral_model is an instance of the gammapy.spectrum.models.PowerLaw2 model, with the parameter values and errors taken from the 3FHL catalog.

Let’s plot the spectral model in the energy range between 10 GeV and 2000 GeV:

[28]:

ax_crab_3fhl = crab_3fhl.spectral_model.plot(
    energy_range=[10, 2000] * u.GeV, energy_power=0
)
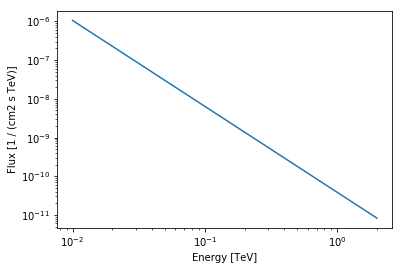
../_images/notebooks_first_steps_59_0.png

We assign the return axes object to variable called ax_crab_3fhl, because we will re-use it later to plot the flux points on top.

To compute the differential flux at 100 GeV we can simply call the model like normal Python function and convert to the desired units:

[29]:

crab_3fhl.spectral_model(100 * u.GeV).to("cm-2 s-1 GeV-1")

[29]:
$$6.3848913 \times 10^{-12} \; \mathrm{\frac{1}{GeV\,s\,cm^{2}}}$$

Next we can compute the integral flux of the Crab between 10 GeV and 2000 GeV:

[30]:

crab_3fhl.spectral_model.integral(emin=10 * u.GeV, emax=2000 * u.GeV).to(
    "cm-2 s-1"
)

[30]:
$$8.6745734 \times 10^{-9} \; \mathrm{\frac{1}{s\,cm^{2}}}$$

We can easily convince ourself, that it corresponds to the value given in the Fermi-LAT 3FHL catalog:

[31]:

crab_3fhl.data["Flux"]

[31]:
$$8.6589091 \times 10^{-9} \; \mathrm{\frac{1}{s\,cm^{2}}}$$

In addition we can compute the energy flux between 10 GeV and 2000 GeV:

[32]:

crab_3fhl.spectral_model.energy_flux(emin=10 * u.GeV, emax=2000 * u.GeV).to(
    "erg cm-2 s-1"
)

[32]:
$$5.3114891 \times 10^{-10} \; \mathrm{\frac{erg}{s\,cm^{2}}}$$

Next we will access the flux points data of the Crab:

[33]:

print(crab_3fhl.flux_points)

FluxPoints(sed_type="flux", n_points=5)

If you want to learn more about the different flux point formats you can read the specification here.

No we can check again the underlying astropy data structure by accessing the .table attribute:

[34]:

crab_3fhl.flux_points.table

[34]:
Table length=5
e_refe_mine_maxfluxflux_errnflux_errpe2dndee2dnde_errne2dnde_errpis_ulflux_ule2dnde_ulsqrt_ts
GeVGeVGeV1 / (cm2 s)1 / (cm2 s)1 / (cm2 s)erg / (cm2 s)erg / (cm2 s)erg / (cm2 s)1 / (cm2 s)erg / (cm2 s)
float64float64float64float32float32float32float32float32float32boolfloat64float64float32
14.14213562373095110.020.05.1698894e-091.3338798e-101.3338798e-101.6420408e-104.236619e-124.236619e-12Falsenannan125.15745
31.62277660168379320.050.02.2450237e-098.671894e-118.671894e-111.1808442e-104.561268e-124.561268e-12Falsenannan88.71535
86.6025403784438650.0150.09.2431746e-105.497474e-115.497474e-111.08686914e-106.464267e-126.464267e-12Falsenannan59.087498
273.8612787525831150.0500.02.7589558e-102.9164688e-113.1360175e-119.2301645e-119.757128e-121.0491635e-11Falsenannan33.076164
1000.0500.02000.06.6840214e-111.4629655e-111.6916293e-116.9011685e-111.5104936e-111.746586e-11Falsenannan15.573053

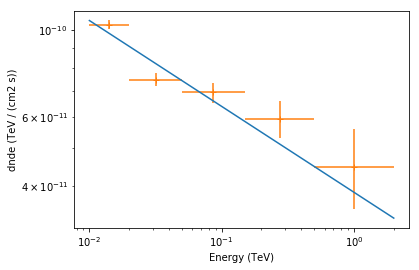
Finally let’s combine spectral model and flux points in a single plot and scale with energy_power=2 to obtain the spectral energy distribution:

[35]:

ax = crab_3fhl.spectral_model.plot(
    energy_range=[10, 2000] * u.GeV, energy_power=2
)
crab_3fhl.flux_points.to_sed_type("dnde").plot(ax=ax, energy_power=2);
../_images/notebooks_first_steps_73_0.png

Exercises

  • Plot the spectral model and flux points for PKS 2155-304 for the 3FGL and 2FHL catalogs. Try to plot the error of the model (aka “Butterfly”) as well. Note this requires the uncertainties package to be installed on your machine.
[36]:

What next?

This was a quick introduction to some of the high-level classes in Astropy and Gammapy.

  • To learn more about those classes, go to the API docs (links are in the introduction at the top).
  • To learn more about other parts of Gammapy (e.g. Fermi-LAT and TeV data analysis), check out the other tutorial notebooks.
  • To see what’s available in Gammapy, browse the Gammapy docs or use the full-text search.
  • If you have any questions, ask on the mailing list.