This is a fixed-text formatted version of a Jupyter notebook

CTA first data challenge logo

CTA data analysis with Gammapy

Introduction

This notebook shows an example how to make a sky image and spectrum for simulated CTA data with Gammapy.

The dataset we will use is three observation runs on the Galactic center. This is a tiny (and thus quick to process and play with and learn) subset of the simulated CTA dataset that was produced for the first data challenge in August 2017.

This notebook can be considered part 2 of the introduction to CTA 1DC analysis. Part one is here:cta_1dc_introduction.ipynb

Setup

As usual, we’ll start with some setup …

[1]:

%matplotlib inline
import matplotlib.pyplot as plt

[2]:

!gammapy info --no-envvar --no-system


Gammapy package:

        path                   : /Users/adonath/github/adonath/gammapy/gammapy
        version                : 0.13


Other packages:

        numpy                  : 1.15.0
        scipy                  : 1.3.0
        matplotlib             : 3.1.1
        cython                 : 0.29.12
        astropy                : 3.2.1
        astropy_healpix        : 0.4
        reproject              : 0.4
        sherpa                 : 4.11.0
        pytest                 : 5.0.1
        sphinx                 : 1.8.5
        healpy                 : 1.12.9
        regions                : 0.4
        iminuit                : 1.3.7
        naima                  : 0.8.3
        uncertainties          : 3.1.1


[3]:

import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from astropy.convolution import Gaussian2DKernel
from regions import CircleSkyRegion
from gammapy.utils.fitting import Fit
from gammapy.data import DataStore
from gammapy.spectrum import (
    SpectrumExtraction,
    models,
    FluxPointsEstimator,
    FluxPointsDataset,
)
from gammapy.maps import MapAxis, WcsNDMap, WcsGeom
from gammapy.cube import MapMaker
from gammapy.background import ReflectedRegionsBackgroundEstimator
from gammapy.detect import TSMapEstimator, find_peaks

[4]:

# Configure the logger, so that the spectral analysis
# isn't so chatty about what it's doing.
import logging

logging.basicConfig()
log = logging.getLogger("gammapy.spectrum")
log.setLevel(logging.ERROR)

Select observations

Like explained in cta_1dc_introduction.ipynb, a Gammapy analysis usually starts by creating a DataStore and selecting observations.

This is shown in detail in the other notebook, here we just pick three observations near the galactic center.

[5]:

data_store = DataStore.from_dir("$GAMMAPY_DATA/cta-1dc/index/gps")

[6]:

# Just as a reminder: this is how to select observations
# from astropy.coordinates import SkyCoord
# table = data_store.obs_table
# pos_obs = SkyCoord(table['GLON_PNT'], table['GLAT_PNT'], frame='galactic', unit='deg')
# pos_target = SkyCoord(0, 0, frame='galactic', unit='deg')
# offset = pos_target.separation(pos_obs).deg
# mask = (1 < offset) & (offset < 2)
# table = table[mask]
# table.show_in_browser(jsviewer=True)

[7]:

obs_id = [110380, 111140, 111159]
observations = data_store.get_observations(obs_id)

[8]:

obs_cols = ["OBS_ID", "GLON_PNT", "GLAT_PNT", "LIVETIME"]
data_store.obs_table.select_obs_id(obs_id)[obs_cols]

[8]:
ObservationTable length=3
OBS_IDGLON_PNTGLAT_PNTLIVETIME
degdegs
int64float64float64float64
110380359.9999912037958-1.2999959379053661764.0
111140358.49998338300741.30000202119542841764.0
1111591.50000565682677411.2999404683352941764.0

Make sky images

Define map geometry

Select the target position and define an ON region for the spectral analysis

[9]:

axis = MapAxis.from_edges(
    np.logspace(-1.0, 1.0, 10), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
    skydir=(0, 0), npix=(500, 400), binsz=0.02, coordsys="GAL", axes=[axis]
)
geom

[9]:

WcsGeom

    axes       : lon, lat, energy
    shape      : (500, 400, 9)
    ndim       : 3
    coordsys   : GAL
    projection : CAR
    center     : 0.0 deg, 0.0 deg
    width      : 10.0 deg x 8.0 deg

Compute images

Exclusion mask currently unused. Remove here or move to later in the tutorial?

[10]:

target_position = SkyCoord(0, 0, unit="deg", frame="galactic")
on_radius = 0.2 * u.deg
on_region = CircleSkyRegion(center=target_position, radius=on_radius)

[11]:

exclusion_mask = geom.to_image().region_mask([on_region], inside=False)
exclusion_mask = WcsNDMap(geom.to_image(), exclusion_mask)
exclusion_mask.plot();
../_images/notebooks_cta_data_analysis_16_0.png 
[12]:

%%time
maker = MapMaker(geom, offset_max="2 deg")
maps = maker.run(observations)
print(maps.keys())

WARNING: Tried to get polar motions for times after IERS data is valid. Defaulting to polar motion from the 50-yr mean for those. This may affect precision at the 10s of arcsec level [astropy.coordinates.builtin_frames.utils]
WARNING:astropy:Tried to get polar motions for times after IERS data is valid. Defaulting to polar motion from the 50-yr mean for those. This may affect precision at the 10s of arcsec level

dict_keys(['counts', 'exposure', 'background'])
CPU times: user 4.03 s, sys: 512 ms, total: 4.54 s
Wall time: 4.51 s

[13]:

# The maps are cubes, with an energy axis.
# Let's also make some images:
images = maker.run_images()

excess = images["counts"].copy()
excess.data -= images["background"].data
images["excess"] = excess

Show images

Let’s have a quick look at the images we computed …

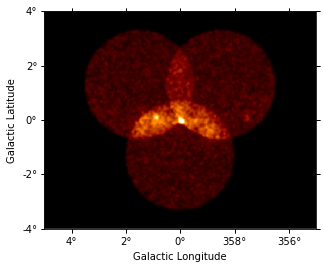
[14]:

images["counts"].smooth(2).plot(vmax=5);
../_images/notebooks_cta_data_analysis_20_0.png 
[15]:

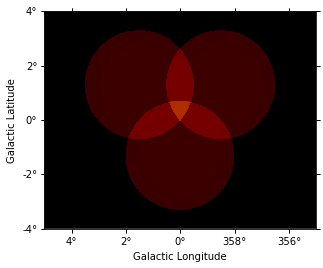
images["background"].plot(vmax=5);
../_images/notebooks_cta_data_analysis_21_0.png 
[16]:

images["excess"].smooth(3).plot(vmax=2);
../_images/notebooks_cta_data_analysis_22_0.png

Source Detection

Use the class gammapy.detect.TSMapEstimator and gammapy.detect.find_peaks to detect sources on the images:

[17]:

kernel = Gaussian2DKernel(1, mode="oversample").array
plt.imshow(kernel);
../_images/notebooks_cta_data_analysis_24_0.png 
[18]:

%%time
ts_image_estimator = TSMapEstimator()
images_ts = ts_image_estimator.run(images, kernel)
print(images_ts.keys())

dict_keys(['ts', 'sqrt_ts', 'flux', 'flux_err', 'flux_ul', 'niter'])
CPU times: user 967 ms, sys: 177 ms, total: 1.14 s
Wall time: 9.96 s

[19]:

sources = find_peaks(images_ts["sqrt_ts"], threshold=8)
sources

[19]:
Table length=2
valuexyradec
degdeg
float32int64int64float64float64
21.387252197266.42400-29.00490
10.282207204266.82019-28.16314
[20]:

source_pos = SkyCoord(sources["ra"], sources["dec"])
source_pos

[20]:

<SkyCoord (ICRS): (ra, dec) in deg
    [(266.42399798, -29.00490483), (266.82018801, -28.16313964)]>

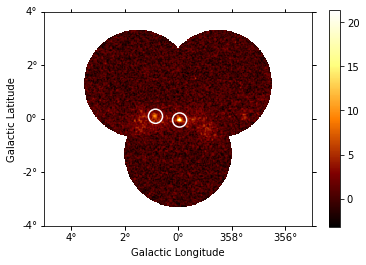
[21]:

# Plot sources on top of significance sky image
images_ts["sqrt_ts"].plot(add_cbar=True)

plt.gca().scatter(
    source_pos.ra.deg,
    source_pos.dec.deg,
    transform=plt.gca().get_transform("icrs"),
    color="none",
    edgecolor="white",
    marker="o",
    s=200,
    lw=1.5,
);
../_images/notebooks_cta_data_analysis_28_0.png

Spatial analysis

See other notebooks for how to run a 3D cube or 2D image based analysis.

Spectrum

We’ll run a spectral analysis using the classical reflected regions background estimation method, and using the on-off (often called WSTAT) likelihood function.

Extraction

The first step is to “extract” the spectrum, i.e. 1-dimensional counts and exposure and background vectors, as well as an energy dispersion matrix from the data and IRFs.

[22]:

%%time
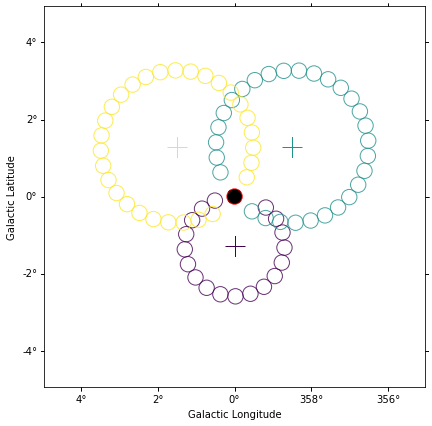
bkg_estimator = ReflectedRegionsBackgroundEstimator(
    observations=observations,
    on_region=on_region,
    exclusion_mask=exclusion_mask,
)
bkg_estimator.run()
bkg_estimate = bkg_estimator.result
bkg_estimator.plot();

CPU times: user 4.67 s, sys: 204 ms, total: 4.87 s
Wall time: 4.86 s

[22]:

(<Figure size 504x504 with 1 Axes>,
 <matplotlib.axes._subplots.WCSAxesSubplot at 0x1271d18d0>,
 None)
../_images/notebooks_cta_data_analysis_31_2.png 
[23]:

%%time
extract = SpectrumExtraction(
    observations=observations, bkg_estimate=bkg_estimate
)
extract.run()
extract.compute_energy_threshold()

CPU times: user 788 ms, sys: 21.4 ms, total: 809 ms
Wall time: 739 ms

Model fit

The next step is to fit a spectral model, using all data (i.e. a “global” fit, using all energies).

[24]:

%%time
model = models.PowerLaw(
    index=2, amplitude=1e-11 * u.Unit("cm-2 s-1 TeV-1"), reference=1 * u.TeV
)

for dataset in extract.spectrum_observations:
    dataset.model = model

fit = Fit(extract.spectrum_observations)
result = fit.run()
print(result)

OptimizeResult

        backend    : minuit
        method     : minuit
        success    : True
        message    : Optimization terminated successfully.
        nfev       : 75
        total stat : 226.10

CPU times: user 247 ms, sys: 5.19 ms, total: 252 ms
Wall time: 250 ms

Spectral points

Finally, let’s compute spectral points. The method used is to first choose an energy binning, and then to do a 1-dim likelihood fit / profile to compute the flux and flux error.

[25]:

# Flux points are computed on stacked observation
from gammapy.spectrum import SpectrumDatasetOnOffStacker

stacker = SpectrumDatasetOnOffStacker(extract.spectrum_observations)
stacked_obs = stacker.run()

print(stacked_obs)

SpectrumDatasetOnOff

    Total counts                    : 2376
    Total predicted counts          : nan
    Total off counts                : 34922.00

    Effective area min              : 1.60e+06 cm2
    Effective area max              : 6.08e+10 cm2

    Livetime                        : 5.29e+03 s

    Number of total bins            : 72
    Number of fit bins              : 72

    Fit statistic type              : wstat
    Fit statistic value (-2 log(L)) : nan

    Number of parameters            : 0
    Number of free parameters       : 0

    Acceptance mean:                : 1.0


[26]:

e_edges = np.logspace(0, 1.5, 5) * u.TeV

stacked_obs.model = model

fpe = FluxPointsEstimator(datasets=[dataset], e_edges=e_edges)
flux_points = fpe.run()
flux_points.table_formatted

[26]:
Table length=4
e_refe_mine_maxref_dnderef_fluxref_efluxref_e2dndenormloglikenorm_errcounts [1]norm_errpnorm_errnnorm_ulsqrt_tstsnorm_scan [11]dloglike_scan [11]dndednde_uldnde_errdnde_errpdnde_errn
TeVTeVTeV1 / (cm2 s TeV)1 / (cm2 s)TeV / (cm2 s)TeV / (cm2 s)1 / (cm2 s TeV)1 / (cm2 s TeV)1 / (cm2 s TeV)1 / (cm2 s TeV)1 / (cm2 s TeV)
float64float64float64float64float64float64float64float64float64float64int64float64float64float64float64float64float64float64float64float64float64float64float64
1.5651.0002.4481.110e-121.634e-122.437e-122.717e-120.9252.2860.191370.2020.1811.3507.47555.8810.200 .. 5.00027.984966330999157 .. 150.568763834041531.026e-121.498e-122.122e-132.243e-132.006e-13
3.8312.4485.9951.513e-135.455e-131.992e-122.221e-120.8461.9560.205230.2200.1911.3156.90647.6970.200 .. 5.00020.634204716592542 .. 120.321864619560341.280e-131.990e-133.106e-143.324e-142.896e-14
8.7995.99512.9152.379e-141.666e-131.415e-121.842e-120.56110.8220.26870.3010.2371.2353.1239.7520.200 .. 5.00013.581463576745378 .. 71.416396622609161.333e-142.938e-146.369e-157.162e-155.627e-15
20.20912.91531.6233.740e-157.113e-141.370e-121.528e-120.5455.5520.35130.4220.2871.5412.7617.6230.200 .. 5.0007.176513233902151 .. 36.717194682218552.037e-155.764e-151.315e-151.580e-151.073e-15

Plot

Let’s plot the spectral model and points. You could do it directly, but there is a helper class. Note that a spectral uncertainty band, a “butterfly” is drawn, but it is very thin, i.e. barely visible.

[27]:

model.parameters.covariance = result.parameters.covariance
flux_points_dataset = FluxPointsDataset(data=flux_points, model=model)

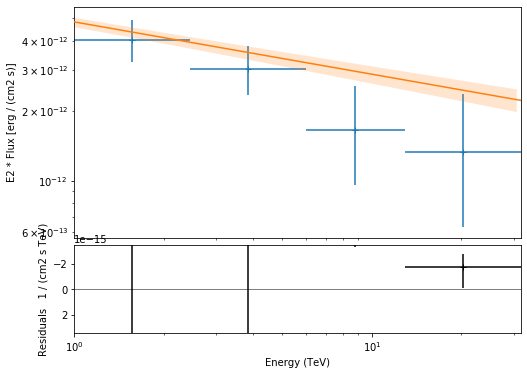
[28]:

plt.figure(figsize=(8, 6))
flux_points_dataset.peek();
../_images/notebooks_cta_data_analysis_40_0.png

Exercises

  • Re-run the analysis above, varying some analysis parameters, e.g.
    • Select a few other observations
    • Change the energy band for the map
    • Change the spectral model for the fit
    • Change the energy binning for the spectral points
  • Change the target. Make a sky image and spectrum for your favourite source.
    • If you don’t know any, the Crab nebula is the “hello world!” analysis of gamma-ray astronomy.
[29]:

# print('hello world')
# SkyCoord.from_name('crab')

What next?

  • This notebook showed an example of a first CTA analysis with Gammapy, using simulated 1DC data.
  • This was part 2 for CTA 1DC turorial, the first part was here: cta_1dc_introduction.ipynb
  • Let us know if you have any question or issues!