This is a fixed-text formatted version of a Jupyter notebook

Flux point fitting#

Prerequisites#

Context#

Some high level studies do not rely on reduced datasets with their IRFs but directly on higher level products such as flux points. This is not ideal because flux points already contain some hypothesis for the underlying spectral shape and the uncertainties they carry are usually simplified (e.g. symmetric gaussian errors). Yet, this is an efficient way to combine heterogeneous data.

Objective: fit spectral models to combined Fermi-LAT and IACT flux points.

Proposed approach#

Here we will load, the spectral points from Fermi-LAT and TeV catalogs and fit them with various spectral models to find the best representation of the wide band spectrum.

The central class we’re going to use for this example analysis is:

In addition we will work with the following data classes:

And the following spectral model classes:

Setup#

Let us start with the usual IPython notebook and Python imports:

[1]:

%matplotlib inline
import matplotlib.pyplot as plt

[2]:

from astropy import units as u
from gammapy.modeling.models import (
    PowerLawSpectralModel,
    ExpCutoffPowerLawSpectralModel,
    LogParabolaSpectralModel,
    SkyModel,
)
from gammapy.estimators import FluxPoints
from gammapy.datasets import FluxPointsDataset, Datasets
from gammapy.catalog import CATALOG_REGISTRY
from gammapy.modeling import Fit

Load spectral points#

For this analysis we choose to work with the source ‘HESS J1507-622’ and the associated Fermi-LAT sources ‘3FGL J1506.6-6219’ and ‘3FHL J1507.9-6228e’. We load the source catalogs, and then access source of interest by name:

[3]:

catalog_3fgl = CATALOG_REGISTRY.get_cls("3fgl")()
catalog_3fhl = CATALOG_REGISTRY.get_cls("3fhl")()
catalog_gammacat = CATALOG_REGISTRY.get_cls("gamma-cat")()

[4]:

source_fermi_3fgl = catalog_3fgl["3FGL J1506.6-6219"]
source_fermi_3fhl = catalog_3fhl["3FHL J1507.9-6228e"]
source_gammacat = catalog_gammacat["HESS J1507-622"]

The corresponding flux points data can be accessed with .flux_points attribute:

[5]:

dataset_gammacat = FluxPointsDataset(
    data=source_gammacat.flux_points, name="gammacat"
)
dataset_gammacat.data.to_table(sed_type="dnde", formatted=True)

[5]:
Table length=6
e_refdndednde_errpdnde_errnis_ul
TeV1 / (cm2 s TeV)1 / (cm2 s TeV)1 / (cm2 s TeV)
float64float64float64float64bool
0.8612.291e-128.955e-138.705e-13False
1.5626.982e-132.304e-132.204e-13False
2.7641.691e-137.188e-146.759e-14False
4.8927.729e-142.607e-142.401e-14False
9.9891.033e-145.642e-155.063e-15False
27.0407.450e-167.260e-165.721e-16False
[6]:

dataset_3fgl = FluxPointsDataset(
    data=source_fermi_3fgl.flux_points, name="3fgl"
)
dataset_3fgl.data.to_table(sed_type="dnde", formatted=True)

[6]:
Table length=5
e_refe_mine_maxdndednde_errpdnde_errndnde_ulsqrt_tsis_ul
MeVMeVMeV1 / (cm2 MeV s)1 / (cm2 MeV s)1 / (cm2 MeV s)1 / (cm2 MeV s)
float64float64float64float64float64float64float64float32bool
173.205100.000300.0001.798e-105.566e-115.710e-11nan2.843False
547.723300.0001000.0002.171e-131.689e-12nan3.595e-120.000True
1732.0511000.0003000.0002.528e-131.058e-139.991e-14nan2.661False
5477.2263000.00010000.0002.654e-148.936e-157.932e-15nan4.265False
31622.77710000.000100000.0001.274e-154.237e-163.658e-16nan5.774False
[7]:

dataset_3fhl = FluxPointsDataset(
    data=source_fermi_3fhl.flux_points, name="3fhl"
)
dataset_3fhl.data.to_table(sed_type="dnde", formatted=True)

[7]:
Table length=5
e_refe_mine_maxdndednde_errpdnde_errndnde_ulsqrt_tsis_ul
GeVGeVGeV1 / (cm2 GeV s)1 / (cm2 GeV s)1 / (cm2 GeV s)1 / (cm2 GeV s)
float64float64float64float64float64float64float64float32bool
14.14210.00020.0009.288e-122.343e-122.128e-12nan5.660False
31.62320.00050.0002.777e-126.572e-135.818e-13nan6.940False
86.60350.000150.0002.335e-131.055e-138.554e-14nan3.835False
273.861150.000500.0006.411e-142.697e-142.133e-14nan5.697False
1000.000500.0002000.0009.188e-214.034e-15nan8.068e-150.000True

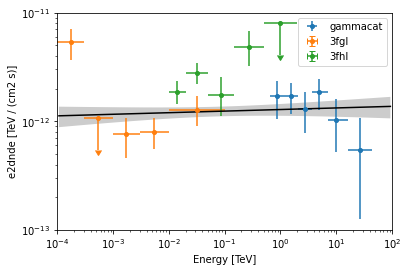
Power Law Fit#

First we start with fitting a simple gammapy.modeling.models.PowerLawSpectralModel.

[8]:

pwl = PowerLawSpectralModel(
    index=2, amplitude="1e-12 cm-2 s-1 TeV-1", reference="1 TeV"
)
model = SkyModel(spectral_model=pwl, name="j1507-pl")

After creating the model we run the fit by passing the 'flux_points' and 'model' objects:

[9]:

datasets = Datasets([dataset_gammacat, dataset_3fgl, dataset_3fhl])
datasets.models = model
print(datasets)

Datasets
--------

Dataset 0:

  Type       : FluxPointsDataset
  Name       : gammacat
  Instrument :
  Models     : ['j1507-pl']

Dataset 1:

  Type       : FluxPointsDataset
  Name       : 3fgl
  Instrument :
  Models     : ['j1507-pl']

Dataset 2:

  Type       : FluxPointsDataset
  Name       : 3fhl
  Instrument :
  Models     : ['j1507-pl']



[10]:

fitter = Fit()
result_pwl = fitter.run(datasets=datasets)

And print the result:

[11]:

print(result_pwl)

OptimizeResult

        backend    : minuit
        method     : migrad
        success    : True
        message    : Optimization terminated successfully.
        nfev       : 40
        total stat : 28.29

CovarianceResult

        backend    : minuit
        method     : hesse
        success    : True
        message    : Hesse terminated successfully.


[12]:

print(model)

SkyModel

  Name                      : j1507-pl
  Datasets names            : None
  Spectral model type       : PowerLawSpectralModel
  Spatial  model type       :
  Temporal model type       :
  Parameters:
    index                         :      1.985   +/-    0.03
    amplitude                     :   1.28e-12   +/- 1.6e-13 1 / (cm2 s TeV)
    reference             (frozen):      1.000       TeV

Finally we plot the data points and the best fit model:

[13]:

ax = plt.subplot()
ax.yaxis.set_units(u.Unit("TeV cm-2 s-1"))

kwargs = {"ax": ax, "sed_type": "e2dnde"}

for d in datasets:
    d.data.plot(label=d.name, **kwargs)

energy_bounds = [1e-4, 1e2] * u.TeV
pwl.plot(energy_bounds=energy_bounds, color="k", **kwargs)
pwl.plot_error(energy_bounds=energy_bounds, **kwargs)
ax.set_ylim(1e-13, 1e-11)
ax.set_xlim(energy_bounds)
ax.legend()

[13]:

<matplotlib.legend.Legend at 0x13f3cbb20>
../../../_images/tutorials_analysis_1D_sed_fitting_21_1.png

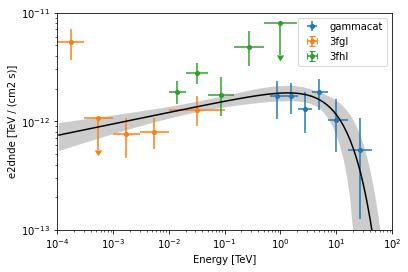
Exponential Cut-Off Powerlaw Fit#

Next we fit an gammapy.modeling.models.ExpCutoffPowerLawSpectralModel law to the data.

[14]:

ecpl = ExpCutoffPowerLawSpectralModel(
    index=1.8,
    amplitude="2e-12 cm-2 s-1 TeV-1",
    reference="1 TeV",
    lambda_="0.1 TeV-1",
)
model = SkyModel(spectral_model=ecpl, name="j1507-ecpl")

We run the fitter again by passing the flux points and the model instance:

[15]:

datasets.models = model
result_ecpl = fitter.run(datasets=datasets)
print(model)

SkyModel

  Name                      : j1507-ecpl
  Datasets names            : None
  Spectral model type       : ExpCutoffPowerLawSpectralModel
  Spatial  model type       :
  Temporal model type       :
  Parameters:
    index                         :      1.894   +/-    0.05
    amplitude                     :   1.96e-12   +/- 3.9e-13 1 / (cm2 s TeV)
    reference             (frozen):      1.000       TeV
    lambda_                       :      0.078   +/-    0.05 1 / TeV
    alpha                 (frozen):      1.000

We plot the data and best fit model:

[16]:

ax = plt.subplot()

kwargs = {"ax": ax, "sed_type": "e2dnde"}

ax.yaxis.set_units(u.Unit("TeV cm-2 s-1"))

for d in datasets:
    d.data.plot(label=d.name, **kwargs)

ecpl.plot(energy_bounds=energy_bounds, color="k", **kwargs)
ecpl.plot_error(energy_bounds=energy_bounds, **kwargs)
ax.set_ylim(1e-13, 1e-11)
ax.set_xlim(energy_bounds)
ax.legend()

[16]:

<matplotlib.legend.Legend at 0x13f8b3b80>
../../../_images/tutorials_analysis_1D_sed_fitting_27_1.png

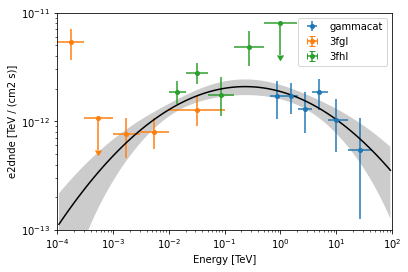
Log-Parabola Fit#

Finally we try to fit a gammapy.modeling.models.LogParabolaSpectralModel model:

[17]:

log_parabola = LogParabolaSpectralModel(
    alpha=2, amplitude="1e-12 cm-2 s-1 TeV-1", reference="1 TeV", beta=0.1
)
model = SkyModel(spectral_model=log_parabola, name="j1507-lp")

[18]:

datasets.models = model
result_log_parabola = fitter.run(datasets=datasets)
print(model)

SkyModel

  Name                      : j1507-lp
  Datasets names            : None
  Spectral model type       : LogParabolaSpectralModel
  Spatial  model type       :
  Temporal model type       :
  Parameters:
    amplitude                     :   1.88e-12   +/- 2.8e-13 1 / (cm2 s TeV)
    reference             (frozen):      1.000       TeV
    alpha                         :      2.144   +/-    0.07
    beta                          :      0.049   +/-    0.02



[19]:

ax = plt.subplot()

kwargs = {"ax": ax, "sed_type": "e2dnde"}

ax.yaxis.set_units(u.Unit("TeV cm-2 s-1"))

for d in datasets:
    d.data.plot(label=d.name, **kwargs)

log_parabola.plot(energy_bounds=energy_bounds, color="k", **kwargs)
log_parabola.plot_error(energy_bounds=energy_bounds, **kwargs)
ax.set_ylim(1e-13, 1e-11)
ax.set_xlim(energy_bounds)
ax.legend()

[19]:

<matplotlib.legend.Legend at 0x13ead8c40>
../../../_images/tutorials_analysis_1D_sed_fitting_31_1.png

Exercises#

What next?#

This was an introduction to SED fitting in Gammapy.

  • If you would like to learn how to perform a full Poisson maximum likelihood spectral fit, please check out the spectrum analysis tutorial.

  • To learn how to combine heterogeneous datasets to perform a multi-instrument forward-folding fit see the MWL analysis tutorial

[ ]: