NaimaModel

class gammapy.spectrum.models.NaimaModel(radiative_model, distance=<Quantity 1. kpc>, seed=None)

Bases: gammapy.spectrum.models.SpectralModel

A wrapper for Naima models.

This class provides an interface with the models defined in the models module. The model accepts as a positional argument a Naima radiative model instance, used to compute the non-thermal emission from populations of relativistic electrons or protons due to interactions with the ISM or with radiation and magnetic fields.

One of the advantages provided by this class consists in the possibility of performing a maximum likelihood spectral fit of the model’s parameters directly on observations, as opposed to the MCMC fit to flux points featured in Naima. All the parameters defining the parent population of charged particles are stored as Parameter and left free by default. In case that the radiative model is ` ~naima.radiative.Synchrotron`, the magnetic field strength may also be fitted. Parameters can be freezed/unfreezed before the fit, and maximum/minimum values can be set to limit the parameters space to the physically interesting region.

Parameters:

radiative_model : BaseRadiative

An instance of a radiative model defined in models

distance : Quantity, optional

Distance to the source. If set to 0, the intrinsic differential luminosity will be returned. Default is 1 kpc

seed : str or list of str, optional

Seed photon field(s) to be considered for the radiative_model flux computation, in case of a InverseCompton model. It can be a subset of the seed_photon_fields list defining the radiative_model. Default is the whole list of photon fields

Examples

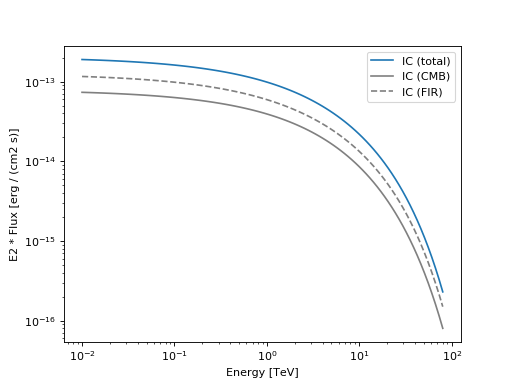
Create and plot a spectral model that convolves an ExponentialCutoffPowerLaw electron distribution with an InverseCompton radiative model, in the presence of multiple seed photon fields.

import naima
from gammapy.spectrum.models import NaimaModel
import astropy.units as u
import matplotlib.pyplot as plt

particle_distribution = naima.models.ExponentialCutoffPowerLaw(1e30 / u.eV, 10 * u.TeV, 3.0, 30 * u.TeV)
radiative_model = naima.radiative.InverseCompton(
    particle_distribution,
    seed_photon_fields=[
        "CMB",
        ["FIR", 26.5 * u.K, 0.415 * u.eV / u.cm ** 3],
    ],
    Eemin=100 * u.GeV,
)

model = NaimaModel(radiative_model, distance=1.5 * u.kpc)

opts = {
    "energy_range" : [10 * u.GeV, 80 * u.TeV],
    "energy_power" : 2,
    "flux_unit" : "erg-1 cm-2 s-1",
}

# Plot the total inverse Compton emission
model.plot(label='IC (total)', **opts)

# Plot the separate contributions from each seed photon field
for seed, ls in zip(['CMB','FIR'], ['-','--']):
    model = NaimaModel(radiative_model, seed=seed, distance=1.5 * u.kpc)
    model.plot(label="IC ({})".format(seed), ls=ls, color="gray", **opts)

plt.legend(loc='best')
plt.show()

(png, hires.png, pdf)

Attributes Summary

parameters

Parameters (Parameters)

Methods Summary

__call__(self, energy)	Call self as a function.
copy(self)	A deep copy.
energy_flux(self, emin, emax, \*\*kwargs)	Compute energy flux in given energy range.
energy_flux_error(self, emin, emax, \*\*kwargs)	Compute energy flux in given energy range with error propagation.
evaluate(self, energy, \*\*kwargs)	Evaluate the model.
evaluate_error(self, energy)	Evaluate spectral model with error propagation.
from_dict(data)	Create from dict.
integral(self, emin, emax, \*\*kwargs)	Integrate spectral model numerically.
integral_error(self, emin, emax, \*\*kwargs)	Integrate spectral model numerically with error propagation.
inverse(self, value[, emin, emax])	Return energy for a given function value of the spectral model.
plot(self, energy_range[, ax, energy_unit, …])	Plot spectral model curve.
plot_error(self, energy_range[, ax, …])	Plot spectral model error band.
spectral_index(self, energy[, epsilon])	Compute spectral index at given energy.
to_dict(self[, selection])

Attributes Documentation

parameters

Parameters (Parameters)

Methods Documentation

__call__(self, energy)

Call self as a function.

copy(self)

A deep copy.

energy_flux(self, emin, emax, **kwargs)

Compute energy flux in given energy range.

\[G(E_{min}, E_{max}) = \int_{E_{min}}^{E_{max}} E \phi(E) dE\]

Parameters:

emin, emax : Quantity

Lower and upper bound of integration range.

**kwargs : dict

Keyword arguments passed to func:integrate_spectrum

energy_flux_error(self, emin, emax, **kwargs)

Compute energy flux in given energy range with error propagation.

\[G(E_{min}, E_{max}) = \int_{E_{min}}^{E_{max}} E \phi(E) dE\]

Parameters:

emin, emax : Quantity

Lower bound of integration range.

**kwargs : dict

Keyword arguments passed to integrate_spectrum()

Returns:

energy_flux, energy_flux_error : tuple of Quantity

Tuple of energy flux and energy flux error.

evaluate(self, energy, **kwargs)

Evaluate the model.

evaluate_error(self, energy)

Evaluate spectral model with error propagation.

Parameters:

energy : Quantity

Energy at which to evaluate

Returns:

flux, flux_error : tuple of Quantity

Tuple of flux and flux error.

classmethod from_dict(data)

Create from dict.

integral(self, emin, emax, **kwargs)

Integrate spectral model numerically.

\[F(E_{min}, E_{max}) = \int_{E_{min}}^{E_{max}} \phi(E) dE\]

If array input for emin and emax is given you have to set intervals=True if you want the integral in each energy bin.

Parameters:

emin, emax : Quantity

Lower and upper bound of integration range.

**kwargs : dict

Keyword arguments passed to integrate_spectrum()

integral_error(self, emin, emax, **kwargs)

Integrate spectral model numerically with error propagation.

Parameters:

emin, emax : Quantity

Lower adn upper bound of integration range.

**kwargs : dict

Keyword arguments passed to func:integrate_spectrum

Returns:

integral, integral_error : tuple of Quantity

Tuple of integral flux and integral flux error.

inverse(self, value, emin=<Quantity 0.1 TeV>, emax=<Quantity 100. TeV>)

Return energy for a given function value of the spectral model.

Calls the scipy.optimize.brentq numerical root finding method.

Parameters:

value : Quantity

Function value of the spectral model.

emin : Quantity

Lower bracket value in case solution is not unique.

emax : Quantity

Upper bracket value in case solution is not unique.

Returns:

energy : Quantity

Energies at which the model has the given value.

plot(self, energy_range, ax=None, energy_unit='TeV', flux_unit='cm-2 s-1 TeV-1', energy_power=0, n_points=100, **kwargs)

Plot spectral model curve.

kwargs are forwarded to matplotlib.pyplot.plot

By default a log-log scaling of the axes is used, if you want to change the y axis scaling to linear you can use:

from gammapy.spectrum.models import ExponentialCutoffPowerLaw
from astropy import units as u

pwl = ExponentialCutoffPowerLaw()
ax = pwl.plot(energy_range=(0.1, 100) * u.TeV)
ax.set_yscale('linear')

Parameters:

ax : Axes, optional

Axis

energy_range : Quantity

Plot range

energy_unit : str, Unit, optional

Unit of the energy axis

flux_unit : str, Unit, optional

Unit of the flux axis

energy_power : int, optional

Power of energy to multiply flux axis with

n_points : int, optional

Number of evaluation nodes

Returns:

ax : Axes, optional

Axis

plot_error(self, energy_range, ax=None, energy_unit='TeV', flux_unit='cm-2 s-1 TeV-1', energy_power=0, n_points=100, **kwargs)

Plot spectral model error band.

Note

This method calls ax.set_yscale("log", nonposy='clip') and ax.set_xscale("log", nonposx='clip') to create a log-log representation. The additional argument nonposx='clip' avoids artefacts in the plot, when the error band extends to negative values (see also https://github.com/matplotlib/matplotlib/issues/8623).

When you call plt.loglog() or plt.semilogy() explicitely in your plotting code and the error band extends to negative values, it is not shown correctly. To circumvent this issue also use plt.loglog(nonposx='clip', nonposy='clip') or plt.semilogy(nonposy='clip').

Parameters:

ax : Axes, optional

Axis

energy_range : Quantity

Plot range

energy_unit : str, Unit, optional

Unit of the energy axis

flux_unit : str, Unit, optional

Unit of the flux axis

energy_power : int, optional

Power of energy to multiply flux axis with

n_points : int, optional

Number of evaluation nodes

**kwargs : dict

Keyword arguments forwarded to matplotlib.pyplot.fill_between

Returns:

ax : Axes, optional

Axis

spectral_index(self, energy, epsilon=1e-05)

Compute spectral index at given energy.

Parameters:

energy : Quantity

Energy at which to estimate the index

epsilon : float

Fractional energy increment to use for determining the spectral index.

Returns:

index : float

Estimated spectral index.

to_dict(self, selection='all')