This is a fixed-text formatted version of a Jupyter notebook
You can contribute with your own notebooks in this GitHub repository.
Source files: spectrum_simulation.ipynb | spectrum_simulation.py
Spectrum simulation¶
Prerequisites¶
Knowledge of spectral extraction and datasets used in gammapy, see for instance the spectral analysis tutorial
Context¶
To simulate a specific observation, it is not always necessary to simulate the full photon list. For many uses cases, simulating directly a reduced binned dataset is enough: the IRFs reduced in the correct geometry are combined with a source model to predict an actual number of counts per bin. The latter is then used to simulate a reduced dataset using Poisson probability distribution.
This can be done to check the feasibility of a measurement, to test whether fitted parameters really provide a good fit to the data etc.
Here we will see how to perform a 1D spectral simulation of a CTA observation, in particular, we will generate OFF observations following the template background stored in the CTA IRFs.
Objective: simulate a number of spectral ON-OFF observations of a source with a power-law spectral model with CTA using the CTA 1DC response, fit them with the assumed spectral model and check that the distribution of fitted parameters is consistent with the input values.
Proposed approach:¶
We will use the following classes:
Setup¶
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
[2]:
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord, Angle
from regions import CircleSkyRegion
from gammapy.spectrum import (
SpectrumDatasetOnOff,
SpectrumDataset,
SpectrumDatasetMaker,
)
from gammapy.modeling import Fit, Parameter
from gammapy.modeling.models import (
PowerLawSpectralModel,
SpectralModel,
SkyModel,
)
from gammapy.irf import load_cta_irfs
from gammapy.data import Observation
from gammapy.maps import MapAxis
Simulation of a single spectrum¶
To do a simulation, we need to define the observational parameters like the livetime, the offset, the assumed integration radius, the energy range to perform the simulation for and the choice of spectral model. We then use an in-memory observation which is convolved with the IRFs to get the predicted number of counts. This is Poission fluctuated using the fake() to get the simulated counts for each observation.
[3]:
# Define simulation parameters parameters
livetime = 1 * u.h
pointing = SkyCoord(0, 0, unit="deg", frame="galactic")
offset = 0.5 * u.deg
# Reconstructed and true energy axis
energy_axis = MapAxis.from_edges(
np.logspace(-0.5, 1.0, 10), unit="TeV", name="energy", interp="log"
)
energy_axis_true = MapAxis.from_edges(
np.logspace(-1.2, 2.0, 31), unit="TeV", name="energy", interp="log"
)
on_region_radius = Angle("0.11 deg")
on_region = CircleSkyRegion(center=pointing, radius=on_region_radius)
[4]:
# Define spectral model - a simple Power Law in this case
model_simu = PowerLawSpectralModel(
index=3.0,
amplitude=2.5e-12 * u.Unit("cm-2 s-1 TeV-1"),
reference=1 * u.TeV,
)
print(model_simu)
# we set the sky model used in the dataset
model = SkyModel(spectral_model=model_simu)
PowerLawSpectralModel
name value error unit min max frozen
--------- --------- ----- -------------- --- --- ------
index 3.000e+00 nan nan nan False
amplitude 2.500e-12 nan cm-2 s-1 TeV-1 nan nan False
reference 1.000e+00 nan TeV nan nan True
[5]:
# Load the IRFs
# In this simulation, we use the CTA-1DC irfs shipped with gammapy.
irfs = load_cta_irfs(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
[6]:
obs = Observation.create(pointing=pointing, livetime=livetime, irfs=irfs)
print(obs)
Observation
obs id : 0
tstart : 51544.00
tstop : 51544.04
duration : 3600.00 s
pointing (icrs) : 266.4 deg, -28.9 deg
deadtime fraction : 0.0%
WARNING: AstropyDeprecationWarning: The truth value of a Quantity is ambiguous. In the future this will raise a ValueError. [astropy.units.quantity]
[7]:
# Make the SpectrumDataset
dataset_empty = SpectrumDataset.create(
e_reco=energy_axis.edges, e_true=energy_axis_true.edges, region=on_region
)
maker = SpectrumDatasetMaker(selection=["aeff", "edisp", "background"])
dataset = maker.run(dataset_empty, obs)
[8]:
# Set the model on the dataset, and fake
dataset.model = model
dataset.fake(random_state=42)
print(dataset)
SpectrumDataset
---------------
Name : Y03hV6Th
Total counts : 16
Total predicted counts : nan
Total background counts : 22.35
Effective area min : 8.16e+04 m2
Effective area max : 5.08e+06 m2
Livetime : 3.60e+03 s
Number of total bins : 9
Number of fit bins : 9
Fit statistic type : cash
Fit statistic value (-2 log(L)) : nan
Number of parameters : 0
Number of free parameters : 0
You can see that backgound counts are now simulated
OnOff analysis¶
To do OnOff spectral analysis, which is the usual science case, the standard would be to use SpectrumDatasetOnOff, which uses the acceptance to fake off-counts
[9]:
dataset_onoff = SpectrumDatasetOnOff(
aeff=dataset.aeff,
edisp=dataset.edisp,
models=model,
livetime=livetime,
acceptance=1,
acceptance_off=5,
)
dataset_onoff.fake(background_model=dataset.background)
print(dataset_onoff)
SpectrumDatasetOnOff
--------------------
Name : G_Ggp0ls
Total counts : 278
Total predicted counts : 298.06
Total off counts : 129.00
Total background counts : 25.80
Effective area min : 8.16e+04 m2
Effective area max : 5.08e+06 m2
Livetime : 1.00e+00 h
Acceptance mean: : 1.0
Number of total bins : 9
Number of fit bins : 9
Fit statistic type : wstat
Fit statistic value (-2 log(L)) : 6.66
Number of parameters : 3
Number of free parameters : 2
Component 0: SkyModel
Name : E_hrDUXC
Spectral model type : PowerLawSpectralModel
Spatial model type : None
Temporal model type :
Parameters:
index : 3.000
amplitude : 2.50e-12 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
You can see that off counts are now simulated as well. We now simulate several spectra using the same set of observation conditions.
[10]:
%%time
n_obs = 100
datasets = []
for idx in range(n_obs):
dataset_onoff.fake(
random_state=idx,
background_model=dataset.background,
name=f"obs_{idx}",
)
datasets.append(dataset_onoff.copy())
CPU times: user 220 ms, sys: 4.82 ms, total: 224 ms
Wall time: 228 ms
Before moving on to the fit let’s have a look at the simulated observations.
[11]:
n_on = [dataset.counts.data.sum() for dataset in datasets]
n_off = [dataset.counts_off.data.sum() for dataset in datasets]
excess = [dataset.excess.data.sum() for dataset in datasets]
fix, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].hist(n_on)
axes[0].set_xlabel("n_on")
axes[1].hist(n_off)
axes[1].set_xlabel("n_off")
axes[2].hist(excess)
axes[2].set_xlabel("excess");

Now, we fit each simulated spectrum individually
[12]:
%%time
results = []
for dataset in datasets:
dataset.models = model.copy()
fit = Fit([dataset])
result = fit.optimize()
results.append(
{
"index": result.parameters["index"].value,
"amplitude": result.parameters["amplitude"].value,
}
)
CPU times: user 4.66 s, sys: 58.7 ms, total: 4.72 s
Wall time: 4.82 s
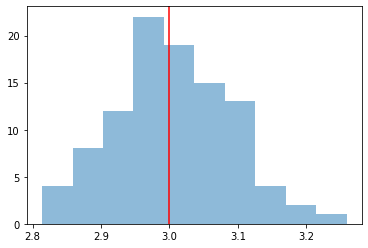
We take a look at the distribution of the fitted indices. This matches very well with the spectrum that we initially injected, index=2.1
[13]:
index = np.array([_["index"] for _ in results])
plt.hist(index, bins=10, alpha=0.5)
plt.axvline(x=model_simu.parameters["index"].value, color="red")
print(f"index: {index.mean()} += {index.std()}")
index: 3.007372509037242 += 0.08556154520735129
Exercises¶
Change the observation time to something longer or shorter. Does the observation and spectrum results change as you expected?
Change the spectral model, e.g. add a cutoff at 5 TeV, or put a steep-spectrum source with spectral index of 4.0
Simulate spectra with the spectral model we just defined. How much observation duration do you need to get back the injected parameters?
[ ]:
