This is a fixed-text formatted version of a Jupyter notebook
You can contribute with your own notebooks in this GitHub repository.
Source files: simulate_3d.ipynb | simulate_3d.py
3D simulation and fitting¶
Prerequisites¶
Knowledge of 3D extraction and datasets used in gammapy, see for instance the first analysis tutorial
Context¶
To simulate a specific observation, it is not always necessary to simulate the full photon list. For many uses cases, simulating directly a reduced binned dataset is enough: the IRFs reduced in the correct geometry are combined with a source model to predict an actual number of counts per bin. The latter is then used to simulate a reduced dataset using Poisson probability distribution.
This can be done to check the feasibility of a measurement (performance / sensitivity study), to test whether fitted parameters really provide a good fit to the data etc.
Here we will see how to perform a 3D simulation of a CTA observation, assuming both the spectral and spatial morphology of an observed source.
Objective: simulate a 3D observation of a source with CTA using the CTA 1DC response and fit it with the assumed source model.
Proposed approach:¶
Here we can’t use the regular observation objects that are connected to a DataStore. Instead we will create a fake gammapy.data.Observation that contain some pointing information and the CTA 1DC IRFs (that are loaded with gammapy.irf.load_cta_irfs).
Then we will create a gammapy.cube.MapDataset geometry and create it with the gammapy.cube.MapDatasetMaker.
Then we will be able to define a model consisting of a gammapy.modeling.models.PowerLawSpectralModel and a gammapy.modeling.models.GaussianSpatialModel. We will assign it to the dataset and fake the count data.
Imports and versions¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from gammapy.irf import load_cta_irfs
from gammapy.maps import WcsGeom, MapAxis
from gammapy.modeling.models import PowerLawSpectralModel
from gammapy.modeling.models import GaussianSpatialModel
from gammapy.modeling.models import SkyModel
from gammapy.cube import MapDataset, MapDatasetMaker, SafeMaskMaker
from gammapy.modeling import Fit
from gammapy.data import Observation
[3]:
!gammapy info --no-envvar --no-dependencies --no-system
Gammapy package:
version : 0.16
path : /Users/adonath/github/adonath/gammapy/gammapy
Simulation¶
We will simulate using the CTA-1DC IRFs shipped with gammapy. Note that for dedictaed CTA simulations, you can simply use `Observation.from_caldb() <>`__ without having to externally load the IRFs
[4]:
# Loading IRFs
irfs = load_cta_irfs(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
[5]:
# Define the observation parameters (typically the observation duration and the pointing position):
livetime = 2.0 * u.hr
pointing = SkyCoord(0, 0, unit="deg", frame="galactic")
[6]:
# Define map geometry for binned simulation
energy_reco = MapAxis.from_edges(
np.logspace(-1.0, 1.0, 10), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
skydir=(0, 0),
binsz=0.02,
width=(6, 6),
frame="galactic",
axes=[energy_reco],
)
# It is usually useful to have a separate binning for the true energy axis
energy_true = MapAxis.from_edges(
np.logspace(-1.5, 1.5, 30), unit="TeV", name="energy", interp="log"
)
[7]:
# Define sky model to used simulate the data.
# Here we use a Gaussian spatial model and a Power Law spectral model.
spatial_model = GaussianSpatialModel(
lon_0="0.2 deg", lat_0="0.1 deg", sigma="0.3 deg", frame="galactic"
)
spectral_model = PowerLawSpectralModel(
index=3, amplitude="1e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)
model_simu = SkyModel(
spatial_model=spatial_model,
spectral_model=spectral_model,
name="model_simu",
)
print(model_simu)
SkyModel
Name : model_simu
Spectral model type : PowerLawSpectralModel
Spatial model type : GaussianSpatialModel
Temporal model type :
Parameters:
lon_0 : 0.200 deg
lat_0 : 0.100 deg
sigma : 0.300 deg
e (frozen) : 0.000
phi (frozen) : 0.000 deg
index : 3.000
amplitude : 1.00e-11 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
Now, comes the main part of dataset simulation. We create an in-memory observation and an empty dataset. We then predict the number of counts for the given model, and Poission fluctuate it using fake() to make a simulated counts maps. Keep in mind that it is important to specify the selection of the maps that you want to produce
[8]:
# Create an in-memory observation
obs = Observation.create(pointing=pointing, livetime=livetime, irfs=irfs)
print(obs)
# Make the MapDataset
empty = MapDataset.create(geom)
maker = MapDatasetMaker(selection=["exposure", "background", "psf", "edisp"])
maker_safe_mask = SafeMaskMaker(methods=["offset-max"], offset_max=4.0 * u.deg)
dataset = maker.run(empty, obs)
dataset = maker_safe_mask.run(dataset, obs)
print(dataset)
Observation
obs id : 0
tstart : 51544.00
tstop : 51544.08
duration : 7200.00 s
pointing (icrs) : 266.4 deg, -28.9 deg
deadtime fraction : 0.0%
WARNING: AstropyDeprecationWarning: The truth value of a Quantity is ambiguous. In the future this will raise a ValueError. [astropy.units.quantity]
MapDataset
----------
Name : RF2-Us73
Total counts : nan
Total predicted counts : 161422.07
Total background counts : 161422.07
Exposure min : 6.41e+07 m2 s
Exposure max : 2.53e+10 m2 s
Number of total bins : 0
Number of fit bins : 804492
Fit statistic type : cash
Fit statistic value (-2 log(L)) : nan
Number of models : 1
Number of parameters : 3
Number of free parameters : 1
[9]:
# Add the model on the dataset and Poission fluctuate
dataset.models = model_simu
dataset.fake()
# Do a print on the dataset - there is now a counts maps
print(dataset)
MapDataset
----------
Name : RF2-Us73
Total counts : 170455
Total predicted counts : 169799.36
Total background counts : 161422.07
Exposure min : 6.41e+07 m2 s
Exposure max : 2.53e+10 m2 s
Number of total bins : 810000
Number of fit bins : 804492
Fit statistic type : cash
Fit statistic value (-2 log(L)) : 563907.97
Number of models : 2
Number of parameters : 11
Number of free parameters : 6
Component 0: SkyModel
Name : model_simu
Spectral model type : PowerLawSpectralModel
Spatial model type : GaussianSpatialModel
Temporal model type :
Parameters:
lon_0 : 0.200 deg
lat_0 : 0.100 deg
sigma : 0.300 deg
e (frozen) : 0.000
phi (frozen) : 0.000 deg
index : 3.000
amplitude : 1.00e-11 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
Now use this dataset as you would in all standard analysis. You can plot the maps, or proceed with your custom analysis. In the next section, we show the standard 3D fitting as in analysis_3d.
[10]:
# To plot, eg, counts:
dataset.counts.smooth(0.05 * u.deg).plot_interactive(
add_cbar=True, stretch="linear"
)

Fit¶
In this section, we do a usual 3D fit with the same model used to simulated the data and see the stability of the simulations. Often, it is useful to simulate many such datasets and look at the distribution of the reconstructed parameters.
[11]:
# Make a copy of the dataset
dataset1 = dataset.copy()
[12]:
# Define sky model to fit the data
spatial_model1 = GaussianSpatialModel(
lon_0="0.1 deg", lat_0="0.1 deg", sigma="0.5 deg", frame="galactic"
)
spectral_model1 = PowerLawSpectralModel(
index=2, amplitude="1e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)
model_fit = SkyModel(
spatial_model=spatial_model1,
spectral_model=spectral_model1,
name="model_fit",
)
dataset1.models = model_fit
print(model_fit)
SkyModel
Name : model_fit
Spectral model type : PowerLawSpectralModel
Spatial model type : GaussianSpatialModel
Temporal model type :
Parameters:
lon_0 : 0.100 deg
lat_0 : 0.100 deg
sigma : 0.500 deg
e (frozen) : 0.000
phi (frozen) : 0.000 deg
index : 2.000
amplitude : 1.00e-11 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
[13]:
# We do not want to fit the background in this case, so we will freeze the parameters
background_model = dataset1.background_model
background_model.parameters["norm"].value = 1.0
background_model.parameters["norm"].frozen = True
background_model.parameters["tilt"].frozen = True
print(background_model)
BackgroundModel
Name : -RiJ-Lqj
Parameters:
norm (frozen) : 1.000
tilt (frozen) : 0.000
reference (frozen) : 1.000 TeV
[14]:
%%time
fit = Fit([dataset1])
result = fit.run(optimize_opts={"print_level": 1})
------------------------------------------------------------------
| FCN = 5.639E+05 | Ncalls=210 (210 total) |
| EDM = 1.27E-05 (Goal: 1E-05) | up = 1.0 |
------------------------------------------------------------------
| Valid Min. | Valid Param. | Above EDM | Reached call limit |
------------------------------------------------------------------
| True | True | False | False |
------------------------------------------------------------------
| Hesse failed | Has cov. | Accurate | Pos. def. | Forced |
------------------------------------------------------------------
| False | True | True | True | False |
------------------------------------------------------------------
CPU times: user 18 s, sys: 1.49 s, total: 19.5 s
Wall time: 19.8 s
[15]:
dataset1.plot_residuals(method="diff/sqrt(model)", vmin=-0.5, vmax=0.5)
[15]:
(<matplotlib.axes._subplots.WCSAxesSubplot at 0x1c1e6adc50>, None)
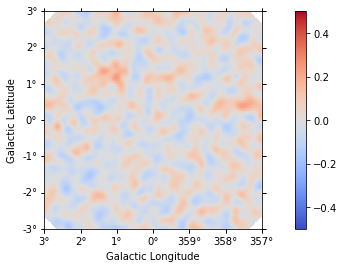
Compare the injected and fitted models:
[16]:
print("True model: \n", model_simu, "\n\n Fitted model: \n", model_fit)
True model:
SkyModel
Name : model_simu
Spectral model type : PowerLawSpectralModel
Spatial model type : GaussianSpatialModel
Temporal model type :
Parameters:
lon_0 : 0.200 deg
lat_0 : 0.100 deg
sigma : 0.300 deg
e (frozen) : 0.000
phi (frozen) : 0.000 deg
index : 3.000
amplitude : 1.00e-11 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
Fitted model:
SkyModel
Name : model_fit
Spectral model type : PowerLawSpectralModel
Spatial model type : GaussianSpatialModel
Temporal model type :
Parameters:
lon_0 : 0.203 deg
lat_0 : 0.099 deg
sigma : 0.298 deg
e (frozen) : 0.000
phi (frozen) : 0.000 deg
index : 3.007
amplitude : 1.01e-11 1 / (cm2 s TeV)
reference (frozen) : 1.000 TeV
Get the errors on the fitted parameters from the parameter table
[17]:
result.parameters.to_table()
[17]:
| name | value | error | unit | min | max | frozen |
|---|---|---|---|---|---|---|
| str9 | float64 | float64 | str14 | float64 | float64 | bool |
| lon_0 | 2.025e-01 | 5.863e-03 | deg | nan | nan | False |
| lat_0 | 9.867e-02 | 5.848e-03 | deg | -9.000e+01 | 9.000e+01 | False |
| sigma | 2.978e-01 | 3.963e-03 | deg | 0.000e+00 | nan | False |
| e | 0.000e+00 | 0.000e+00 | 0.000e+00 | 1.000e+00 | True | |
| phi | 0.000e+00 | 0.000e+00 | deg | nan | nan | True |
| index | 3.007e+00 | 2.006e-02 | nan | nan | False | |
| amplitude | 1.006e-11 | 3.288e-13 | cm-2 s-1 TeV-1 | nan | nan | False |
| reference | 1.000e+00 | 0.000e+00 | TeV | nan | nan | True |
| norm | 1.000e+00 | 0.000e+00 | 0.000e+00 | nan | True | |
| tilt | 0.000e+00 | 0.000e+00 | nan | nan | True | |
| reference | 1.000e+00 | 0.000e+00 | TeV | nan | nan | True |
