Pulsar analysis

Produce a phasogram, phased-resolved maps and spectra for pulsar analysis.

Introduction

This notebook shows how to do a simple pulsar analysis with Gammapy. We will produce a phasogram, a phase-resolved map and a phase-resolved spectrum of the Vela pulsar. In order to build these products, we will use the PhaseBackgroundMaker which takes into account the on and off phase to compute a MapDatasetOnOff and a SpectrumDatasetOnOff in the phase space.

This tutorial uses a simulated run of vel observation from the CTA DC1, which already contains a column for the pulsar phases. The phasing in itself is therefore not show here. It requires specific packages like Tempo2 or PINT. A gammapy recipe shows how to compute phases with PINT in the framework of Gammapy.

Opening the data

Let’s first do the imports and load the only observation containing Vela in the CTA 1DC dataset shipped with Gammapy.

# Remove warnings
import warnings
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
import matplotlib.pyplot as plt

# %matplotlib inline
from IPython.display import display
from gammapy.data import DataStore
from gammapy.datasets import Datasets, FluxPointsDataset, MapDataset, SpectrumDataset
from gammapy.estimators import ExcessMapEstimator, FluxPointsEstimator
from gammapy.makers import (
    MapDatasetMaker,
    PhaseBackgroundMaker,
    SafeMaskMaker,
    SpectrumDatasetMaker,
)
from gammapy.maps import MapAxis, RegionGeom, WcsGeom
from gammapy.modeling import Fit
from gammapy.modeling.models import PowerLawSpectralModel, SkyModel
from gammapy.stats import WStatCountsStatistic
from gammapy.utils.regions import SphericalCircleSkyRegion

warnings.filterwarnings("ignore")

Check setup

from gammapy.utils.check import check_tutorials_setup

check_tutorials_setup()

System:

        python_executable      : /home/runner/work/gammapy-docs/gammapy-docs/gammapy/.tox/build_docs/bin/python
        python_version         : 3.9.18
        machine                : x86_64
        system                 : Linux


Gammapy package:

        version                : 1.2
        path                   : /home/runner/work/gammapy-docs/gammapy-docs/gammapy/.tox/build_docs/lib/python3.9/site-packages/gammapy


Other packages:

        numpy                  : 1.26.4
        scipy                  : 1.12.0
        astropy                : 5.2.2
        regions                : 0.8
        click                  : 8.1.7
        yaml                   : 6.0.1
        IPython                : 8.18.1
        jupyterlab             : not installed
        matplotlib             : 3.8.3
        pandas                 : not installed
        healpy                 : 1.16.6
        iminuit                : 2.25.2
        sherpa                 : 4.16.0
        naima                  : 0.10.0
        emcee                  : 3.1.4
        corner                 : 2.2.2
        ray                    : 2.9.3


Gammapy environment variables:

        GAMMAPY_DATA           : /home/runner/work/gammapy-docs/gammapy-docs/gammapy-datasets/1.2

Load the data store (which is a subset of CTA-DC1 data):

data_store = DataStore.from_dir("$GAMMAPY_DATA/cta-1dc/index/gps")

Define observation ID and print events:

id_obs_vela = [111630]
obs_list_vela = data_store.get_observations(id_obs_vela)
print(obs_list_vela[0].events)

EventList
---------

  Instrument       : None
  Telescope        : CTA
  Obs. ID          : 111630

  Number of events : 101430
  Event rate       : 56.350 1 / s

  Time start       : 59300.833333333336
  Time stop        : 59300.854166666664

  Min. energy      : 3.00e-02 TeV
  Max. energy      : 1.52e+02 TeV
  Median energy    : 1.00e-01 TeV

  Max. offset      : 5.0 deg

Now that we have our observation, let’s select the events in 0.2° radius around the pulsar position.

pos_target = SkyCoord(ra=128.836 * u.deg, dec=-45.176 * u.deg, frame="icrs")
on_radius = 0.2 * u.deg
on_region = SphericalCircleSkyRegion(pos_target, on_radius)

# Apply angular selection
events_vela = obs_list_vela[0].events.select_region(on_region)
print(events_vela)

EventList
---------

  Instrument       : None
  Telescope        : CTA
  Obs. ID          : 111630

  Number of events : 843
  Event rate       : 0.468 1 / s

  Time start       : 59300.833333333336
  Time stop        : 59300.854166666664

  Min. energy      : 3.00e-02 TeV
  Max. energy      : 4.33e+01 TeV
  Median energy    : 1.07e-01 TeV

  Max. offset      : 1.7 deg

Let’s load the phases of the selected events in a dedicated array.

phases = events_vela.table["PHASE"]

# Let's take a look at the first 10 phases
display(phases[:10])

   PHASE
-----------
 0.81847286
 0.45646095
0.111507416
 0.43416595
 0.76837444
  0.3639946
 0.58693695
 0.51095676
  0.5606985
  0.2505703

Phasogram

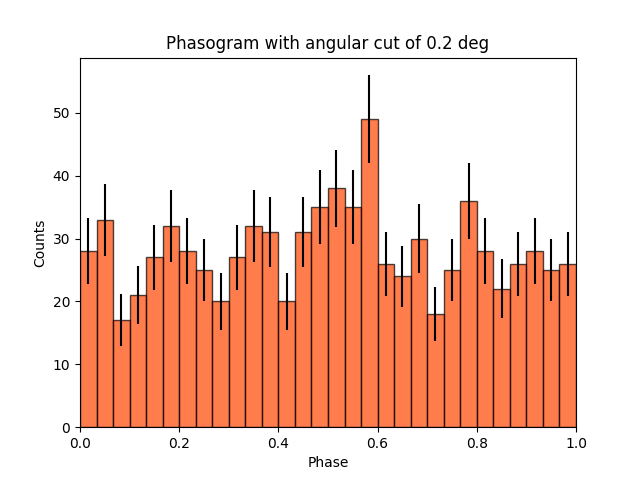
Once we have the phases, we can make a phasogram. A phasogram is a histogram of phases. It works exactly like any other histogram (you can set the binning, evaluate the errors based on the counts in each bin, etc).

nbins = 30
phase_min, phase_max = (0, 1)
values, bin_edges = np.histogram(phases, range=(phase_min, phase_max), bins=nbins)
bin_width = (phase_max - phase_min) / nbins

bin_center = (bin_edges[:-1] + bin_edges[1:]) / 2

# Poissonian uncertainty on each bin
values_err = np.sqrt(values)

fig, ax = plt.subplots()
ax.bar(
    x=bin_center,
    height=values,
    width=bin_width,
    color="orangered",
    alpha=0.7,
    edgecolor="black",
    yerr=values_err,
)
ax.set_xlim(0, 1)
ax.set_xlabel("Phase")
ax.set_ylabel("Counts")
ax.set_title(f"Phasogram with angular cut of {on_radius}")
plt.show()

on_phase_range = (0.5, 0.6)
off_phase_range = (0.7, 1)

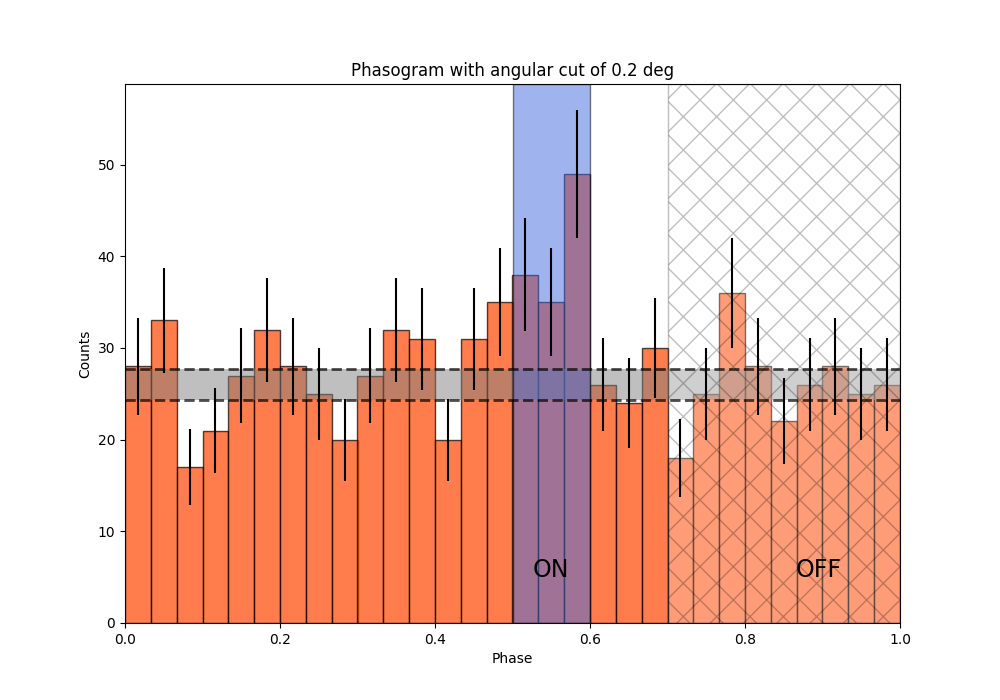
Now let’s add some fancy additions to our phasogram: a patch on the ON- and OFF-phase regions and one for the background level.

# Evaluate background level
mask_off = (off_phase_range[0] < phases) & (phases < off_phase_range[1])

count_bkg = mask_off.sum()
print(f"Number of Off events: {count_bkg}")

# bkg level normalized by the size of the OFF zone (0.3)
bkg = count_bkg / nbins / (off_phase_range[1] - off_phase_range[0])

# error on the background estimation
bkg_err = np.sqrt(count_bkg) / nbins / (off_phase_range[1] - off_phase_range[0])

Number of Off events: 234

Let’s redo the same plot for the basis

fig, ax = plt.subplots(figsize=(10, 7))
ax.bar(
    x=bin_center,
    height=values,
    width=bin_width,
    color="orangered",
    alpha=0.7,
    edgecolor="black",
    yerr=values_err,
)

# Plot background level
x_bkg = np.linspace(0, 1, 50)

kwargs = {"color": "black", "alpha": 0.7, "ls": "--", "lw": 2}

ax.plot(x_bkg, (bkg - bkg_err) * np.ones_like(x_bkg), **kwargs)
ax.plot(x_bkg, (bkg + bkg_err) * np.ones_like(x_bkg), **kwargs)

ax.fill_between(
    x_bkg, bkg - bkg_err, bkg + bkg_err, facecolor="grey", alpha=0.5
)  # grey area for the background level

# Let's make patches for the on and off phase zones
on_patch = ax.axvspan(
    on_phase_range[0], on_phase_range[1], alpha=0.5, color="royalblue", ec="black"
)

off_patch = ax.axvspan(
    off_phase_range[0],
    off_phase_range[1],
    alpha=0.25,
    color="white",
    hatch="x",
    ec="black",
)

# Legends "ON" and "OFF"
ax.text(0.55, 5, "ON", color="black", fontsize=17, ha="center")
ax.text(0.895, 5, "OFF", color="black", fontsize=17, ha="center")
ax.set_xlabel("Phase")
ax.set_ylabel("Counts")
ax.set_xlim(0, 1)
ax.set_title(f"Phasogram with angular cut of {on_radius}")
plt.show()

Make a Li&Ma test over the events

Another thing that we want to do is to compute a Li&Ma test between the on-phase and the off-phase.

# Calculate the ratio between the on-phase and the off-phase
alpha = (on_phase_range[1] - on_phase_range[0]) / (
    off_phase_range[1] - off_phase_range[0]
)

# Select events in the on region
region_events = obs_list_vela[0].events.select_region(on_region)

# Select events in phase space
on_events = region_events.select_parameter("PHASE", band=on_phase_range)
off_events = region_events.select_parameter("PHASE", band=off_phase_range)

# Apply the WStat (Li&Ma statistic)
pulse_stat = WStatCountsStatistic(
    len(on_events.time), len(off_events.time), alpha=alpha
)

print(f"Number of excess counts: {pulse_stat.n_sig}")
print(f"TS: {pulse_stat.ts}")
print(f"Significance: {pulse_stat.sqrt_ts}")

Number of excess counts: 44.00000000000003
TS: 15.211770556360534
Significance: 3.9002269877996247

Phase-resolved map

Now that we have an overview of the phasogram of the pulsar, we can do a phase-resolved sky map : a map of the ON-phase events minus alpha times the OFF-phase events. Alpha is the ratio between the size of the ON-phase zone (here 0.1) and the OFF-phase zone (0.3).

e_true = MapAxis.from_energy_bounds(
    0.003, 10, 6, per_decade=True, unit="TeV", name="energy_true"
)
e_reco = MapAxis.from_energy_bounds(
    0.01, 10, 4, per_decade=True, unit="TeV", name="energy"
)

geom = WcsGeom.create(
    binsz=0.02 * u.deg, skydir=pos_target, width="4 deg", axes=[e_reco]
)

Let’s create an ON-map and an OFF-map:

map_dataset_empty = MapDataset.create(geom=geom, energy_axis_true=e_true)

map_dataset_maker = MapDatasetMaker()
phase_bkg_maker = PhaseBackgroundMaker(
    on_phase=on_phase_range, off_phase=off_phase_range, phase_column_name="PHASE"
)

offset_max = 5 * u.deg
safe_mask_maker = SafeMaskMaker(methods=["offset-max"], offset_max=offset_max)

map_datasets = Datasets()

for obs in obs_list_vela:
    map_dataset = map_dataset_maker.run(map_dataset_empty, obs)
    map_dataset = safe_mask_maker.run(map_dataset, obs)
    map_dataset_on_off = phase_bkg_maker.run(map_dataset, obs)
    map_datasets.append(map_dataset_on_off)

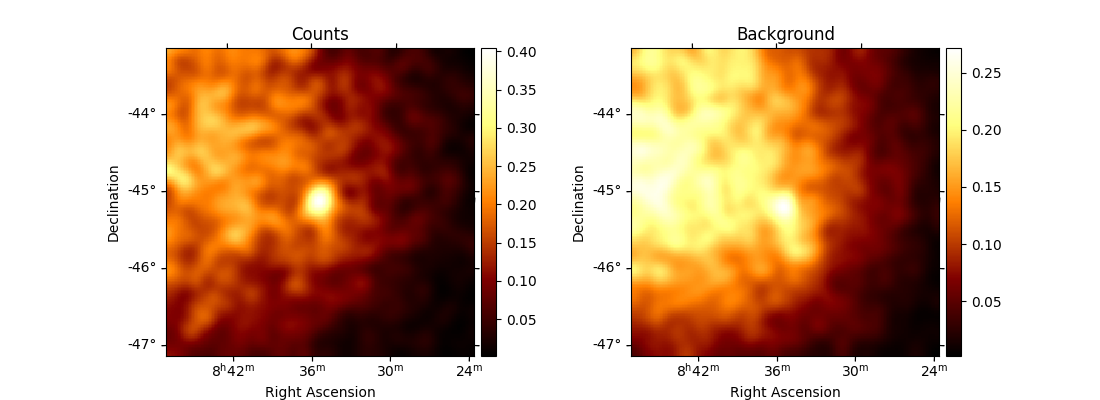
Once the data reduction is done, we can plot the map of the counts-ON (i.e. in the ON-phase) and the map of the background (i.e. the counts-OFF, selected in the OFF-phase, multiplied by alpha). If one wants to plot the counts-OFF instead, background should be replaced by counts_off in the following cell.

counts = (
    map_datasets[0].counts.smooth(kernel="gauss", width=0.1 * u.deg).sum_over_axes()
)
background = (
    map_datasets[0].background.smooth(kernel="gauss", width=0.1 * u.deg).sum_over_axes()
)

fig, (ax1, ax2) = plt.subplots(
    figsize=(11, 4), ncols=2, subplot_kw={"projection": counts.geom.wcs}
)

counts.plot(ax=ax1, add_cbar=True)
ax1.set_title("Counts")

background.plot(ax=ax2, add_cbar=True)
ax2.set_title("Background")

plt.show()

Finally, we can run an ExcessMapEstimator to compute the excess and significance maps.

excess_map_estimator = ExcessMapEstimator(
    correlation_radius="0.2 deg", energy_edges=[50 * u.GeV, 10 * u.TeV]
)
estimator_results = excess_map_estimator.run(dataset=map_datasets[0])

npred_excess = estimator_results.npred_excess
sqrt_ts = estimator_results.sqrt_ts

fig, (ax1, ax2) = plt.subplots(
    figsize=(11, 4), ncols=2, subplot_kw={"projection": npred_excess.geom.wcs}
)

npred_excess.plot(ax=ax1, add_cbar=True)
ax1.set_title("Excess counts")

sqrt_ts.plot(ax=ax2, add_cbar=True)
ax2.set_title("Significance")

plt.show()

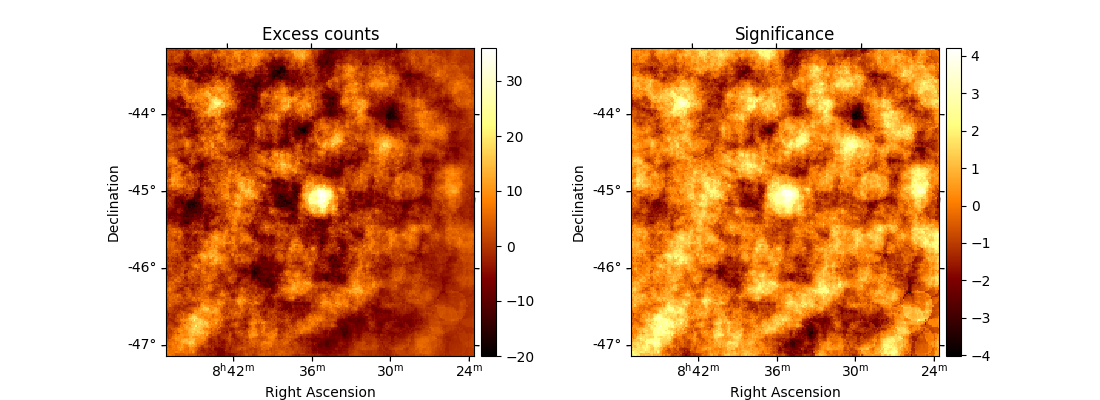
Note that here we are lacking statistic because we only use one run of CTA.

Phase-resolved spectrum

We can also make a phase-resolved spectrum. In order to do that, we are going to use the PhaseBackgroundMaker to create a SpectrumDatasetOnOff with the ON and OFF taken in the phase space. Note that this maker take the ON and OFF in the same spatial region.

Here to create the SpectrumDatasetOnOff, we are going to redo the whole data reduction. However, note that one can use the to_spectrum_dataset() method (with the containment_correction parameter set to True) if such a MapDatasetOnOff has been created as shown above.

e_true = MapAxis.from_energy_bounds(0.003, 10, 100, unit="TeV", name="energy_true")
e_reco = MapAxis.from_energy_bounds(0.01, 10, 30, unit="TeV", name="energy")


geom = RegionGeom.create(region=on_region, axes=[e_reco])

spectrum_dataset_empty = SpectrumDataset.create(geom=geom, energy_axis_true=e_true)

spectrum_dataset_maker = SpectrumDatasetMaker()
phase_bkg_maker = PhaseBackgroundMaker(
    on_phase=on_phase_range, off_phase=off_phase_range, phase_column_name="PHASE"
)

offset_max = 5 * u.deg
safe_mask_maker = SafeMaskMaker(methods=["offset-max"], offset_max=offset_max)

spectrum_datasets = Datasets()

for obs in obs_list_vela:
    spectrum_dataset = spectrum_dataset_maker.run(spectrum_dataset_empty, obs)
    spectrum_dataset = safe_mask_maker.run(spectrum_dataset, obs)
    spectrum_dataset_on_off = phase_bkg_maker.run(spectrum_dataset, obs)
    spectrum_datasets.append(spectrum_dataset_on_off)

Now let’s take a look at the datasets we just created:

spectrum_datasets[0].peek()
plt.show()

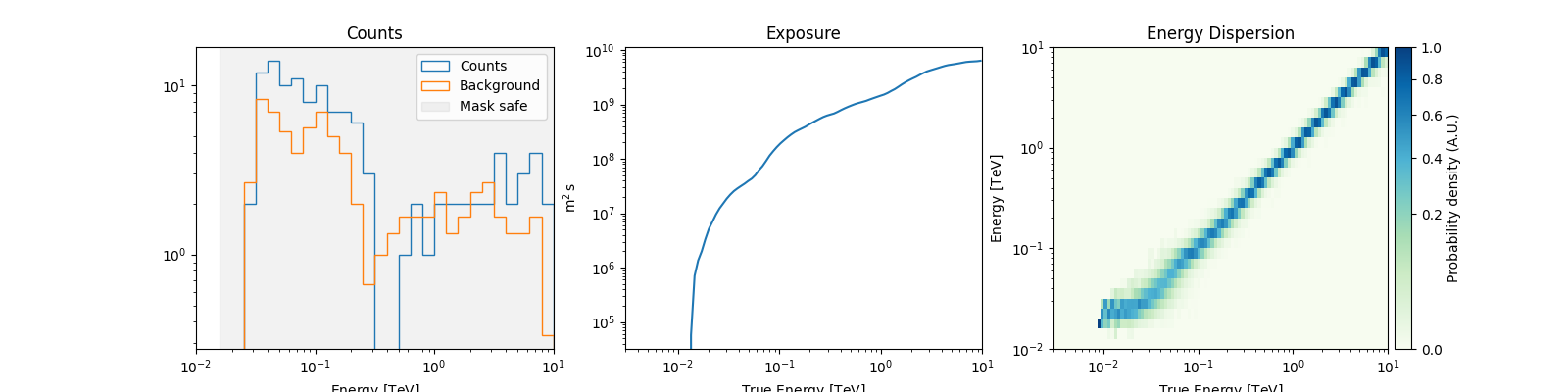
Now we’ll fit a model to the spectrum with the Fit class. First we load a power law model with an initial value for the index and the amplitude and then wo do a likelihood fit. The fit results are printed below.

spectral_model = PowerLawSpectralModel(
    index=4, amplitude="1.3e-9 cm-2 s-1 TeV-1", reference="0.02 TeV"
)
model = SkyModel(spectral_model=spectral_model, name="vela psr")
emin_fit, emax_fit = (0.04 * u.TeV, 0.4 * u.TeV)

mask_fit = geom.energy_mask(energy_min=emin_fit, energy_max=emax_fit)

for dataset in spectrum_datasets:
    dataset.models = model
    dataset.mask_fit = mask_fit

joint_fit = Fit()
joint_result = joint_fit.run(datasets=spectrum_datasets)

print(joint_result)

OptimizeResult

        backend    : minuit
        method     : migrad
        success    : True
        message    : Optimization terminated successfully.
        nfev       : 101
        total stat : 7.07

CovarianceResult

        backend    : minuit
        method     : hesse
        success    : True
        message    : Hesse terminated successfully.

Now you might want to do the stacking here even if in our case there is only one observation which makes it superfluous. We can compute flux points by fitting the norm of the global model in energy bands.

energy_edges = np.logspace(np.log10(0.04), np.log10(0.4), 7) * u.TeV

stack_dataset = spectrum_datasets.stack_reduce()

stack_dataset.models = model

fpe = FluxPointsEstimator(
    energy_edges=energy_edges, source="vela psr", selection_optional="all"
)

flux_points = fpe.run(datasets=[stack_dataset])
flux_points.meta["ts_threshold_ul"] = 1

amplitude_ref = 0.57 * 19.4e-14 * u.Unit("1 / (cm2 s MeV)")
spec_model_true = PowerLawSpectralModel(
    index=4.5, amplitude=amplitude_ref, reference="20 GeV"
)

flux_points_dataset = FluxPointsDataset(data=flux_points, models=model)

Now we can plot.

ax_spectrum, ax_residuals = flux_points_dataset.plot_fit()

ax_spectrum.set_ylim([1e-14, 3e-11])
ax_residuals.set_ylim([-1.7, 1.7])

spec_model_true.plot(
    ax=ax_spectrum,
    energy_bounds=(emin_fit, emax_fit),
    label="Reference model",
    c="black",
    linestyle="dashed",
    energy_power=2,
)

ax_spectrum.legend(loc="best")

plt.show()

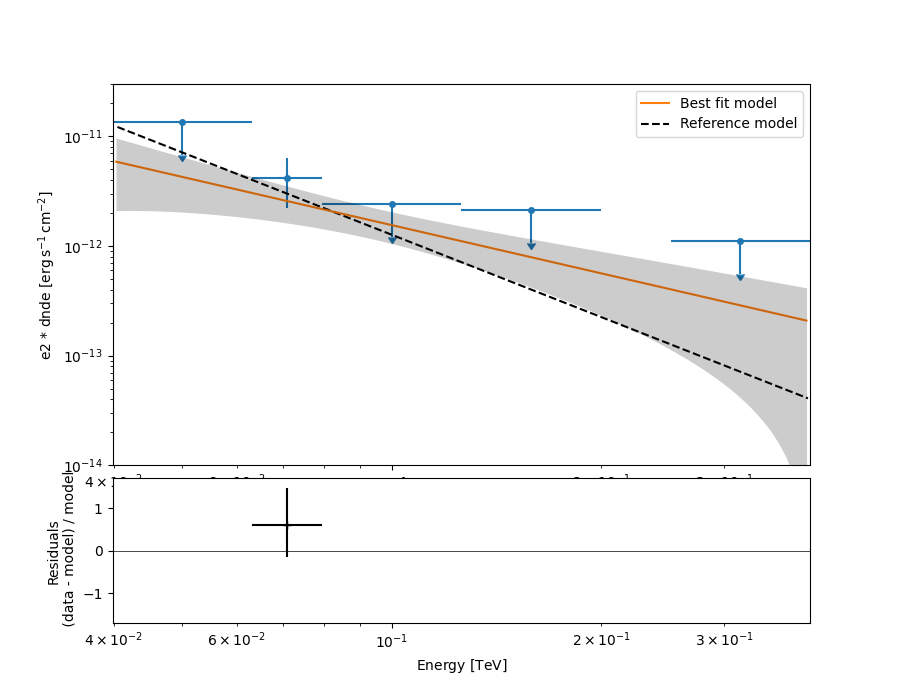
This tutorial suffers a bit from the lack of statistics: there were 9 Vela observations in the CTA DC1 while there is only one here. When done on the 9 observations, the spectral analysis is much better agreement between the input model and the gammapy fit.