Estimators (DL4 to DL5, and DL6)#

The gammapy.estimators submodule contains algorithms and classes for high level flux and significance estimation. This includes estimation flux points, flux maps, flux points, flux profiles and flux light curves. All estimators feature a common API and allow estimating fluxes in bands of reconstructed energy.

General method#

The core of any estimator algorithm is hypothesis testing: a reference model or counts excess is tested against a null hypothesis. From the best fit reference model a flux is derived and a corresponding \(\Delta TS\) value from the difference in fit statistics to the null hypothesis. Assuming one degree of freedom, \(\sqrt{\Delta TS}\) represents an approximation (Wilk’s theorem) of the “classical significance”. In case of a negative best fit flux, e.g. when the background is overestimated, the significance is defined as \(-\sqrt{\Delta TS}\) by convention.

In general the flux can be estimated using two methods:

Based on model fitting: given a (global) best fit model with multiple model components, the flux of the component of interest is re-fitted in the chosen energy, time or spatial region. The new flux is given as a norm with respect to the global reference model. Optionally the free parameters of the other models can be re-optimised (but the other parameters of the source of interest are always kept frozen). This method is also named forward folding.
Based on excess: in the case of having one energy bin, neglecting the PSF and not re-optimising other parameters, one can estimate the significance based on the analytical solution by [LiMa1983]. In this case the “best fit” flux and significance are given by the excess over the null hypothesis. This method is also named backward folding. This method is currently only exposed in the ExcessMapEstimator

Energy edges#

The estimators run on bins of reconstructed energy. The estimator cannot modify the binning of the parent dataset, only group the energy bins. The input energy edges by the user are converted to the nearest parent dataset energy bin values. The estimators select the energy bins from the parent dataset which are closest to the requested energy edges. Hence, the requested edges are used to group the parent dataset energy edges into large bins. Therefore, the input energy edges are not always the same as the output energy bins provided in the final product. If a specific energy binning is required at the estimator level, it should be implemented in the parent dataset geometry (i.e. the dataset energy axis edges should contain the required edges).

Flux quantities#

In case the data is fitted to a single data bin only, e.g. one energy bin Uniformly for both methods most estimators compute the same basic quantities:

Quantity	Definition
norm	Best fit norm with respect to the reference spectral model
norm_err	Symmetric error on the norm derived from the Hessian matrix. Given as absolute difference to the best fit norm.
stat	Fit statistics value of the best fit hypothesis
stat_null	Fit statistics value of the null hypothesis
ts	Difference in fit statistics (`stat - stat_null` )
sqrt_ts	Square root of ts time sign(norm), in case of one degree of freedom (n_dof), corresponds to significance (Wilk’s theorem)
npred	Predicted counts of the best fit hypothesis. Equivalent to correlated counts for backward folding
npred_excess	Predicted excess counts of the best fit hypothesis. Equivalent to correlated excess for backward folding
npred_background	Predicted background counts of the best fit hypothesis. Equivalent to correlated excess for backward folding
n_dof	Number of degrees of freedom. If not explicitly present, assumed to be one

In addition, the following optional quantities can be computed:

Quantity	Definition
norm_errp	Positive error of the norm, given as absolute difference to the best fit norm
norm_errn	Negative error of the norm, given as absolute difference to the best fit norm
norm_ul	Upper limit of the norm
norm_scan	Norm parameter values used for the fit statistic scan
stat_scan	Fit statistics values associated with norm_scan

To compute the error, asymmetric errors as well as upper limits one can specify the arguments n_sigma and n_sigma_ul. The n_sigma arguments are translated into a TS difference assuming ts = n_sigma ** 2.

In addition to the norm values a reference spectral model and energy ranges are given. Using this reference spectral model the norm values can be converted to the following different SED types:

Quantity	Definition
e_ref	Reference energy
e_min	Minimum energy
e_max	Maximum energy
dnde	Differential flux at `e_ref`
flux	Integrated flux between `e_min` and `e_max`
eflux	Integrated energy flux between `e_min` and `e_max`
e2dnde	Differential energy flux at `e_ref`

The same can be applied for the error and upper limit information. More information can be found on the likelihood SED type page.

The FluxPoints and FluxMaps objects can optionally define meta data with the following valid keywords:

Name	Definition
n_sigma	Number of sigma used for error estimation
n_sigma_ul	Number of sigma used for upper limit estimation
ts_threshold_ul	TS threshold to define the use of an upper limit

A note on negative flux and upper limit values:

Note

Gammapy allows for negative flux values and upper limits by default. While those values are physically not valid solutions, they are still valid statistically. Negative flux values either hint at overestimated background levels or underestimated systematic errors in general. Or in case of many measurements, such as pixels in a flux map, they are even statistically expected. For flux points and light curves the amplitude limits (if defined) are taken into account. In future versions of Gammapy it will be possible to account for systematic errors in the likelihood as well. For now the correct interpretation of the results is left to the user.

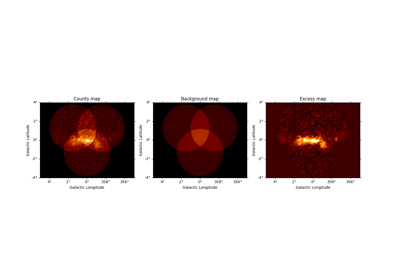
Flux maps#

This how to compute flux maps with the ExcessMapEstimator:

import numpy as np
from gammapy.datasets import MapDataset
from gammapy.estimators import ExcessMapEstimator
from astropy import units as u

dataset = MapDataset.read("$GAMMAPY_DATA/cta-1dc-gc/cta-1dc-gc.fits.gz")

estimator = ExcessMapEstimator(
    correlation_radius="0.1 deg", energy_edges=[0.1, 1, 10] * u.TeV
)

maps = estimator.run(dataset)
print(maps["flux"])

WcsNDMap
<BLANKLINE>
    geom  : WcsGeom
    axes  : ['lon', 'lat', 'energy']
    shape : (320, 240, 2)
    ndim  : 3
    unit  : 1 / (cm2 s)
    dtype : float64
<BLANKLINE>

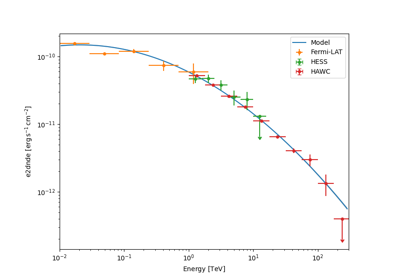
Flux points#

This is how to compute flux points:

from astropy import units as u
from gammapy.datasets import SpectrumDatasetOnOff, Datasets
from gammapy.estimators import FluxPointsEstimator
from gammapy.modeling.models import PowerLawSpectralModel, SkyModel

path = "$GAMMAPY_DATA/joint-crab/spectra/hess/"
dataset_1 = SpectrumDatasetOnOff.read(path + "pha_obs23523.fits")
dataset_2 = SpectrumDatasetOnOff.read(path + "pha_obs23592.fits")

datasets = Datasets([dataset_1, dataset_2])

pwl = PowerLawSpectralModel(index=2, amplitude='1e-12  cm-2 s-1 TeV-1')

datasets.models = SkyModel(spectral_model=pwl, name="crab")

estimator = FluxPointsEstimator(
    source="crab", energy_edges=[0.1, 0.3, 1, 3, 10, 30, 100] * u.TeV
)

# this will run a joint fit of the datasets
fp = estimator.run(datasets)
table = fp.to_table(sed_type="dnde", formatted=True)
# print(table[["e_ref", "dnde", "dnde_err"]])

# or stack the datasets
# fp = estimator.run(datasets.stack_reduce())
table = fp.to_table(sed_type="dnde", formatted=True)
# print(table[["e_ref", "dnde", "dnde_err"]])

Using gammapy.estimators#

Examples using `gammapy.estimators.FluxPointsEstimator`#

Low level API

Spectral analysis

Multi instrument joint 3D and 1D analysis

Basic image exploration and fitting

Flux Profile Estimation

Light curves

Light curves for flares

Simulating and fitting a time varying source

Pulsar analysis

Examples using `gammapy.estimators.LightCurveEstimator`#