SkyEllipse

class gammapy.image.models.SkyEllipse(lon_0, lat_0, semi_major, e, theta, edge='0.01 deg', frame='galactic')

Bases: gammapy.image.models.SkySpatialModel

Constant elliptical model.

\[\begin{split}\phi(\text{lon}, \text{lat}) = \begin{cases} N & \text{for } \,\,\,dist(F_1,P)+dist(F_2,P)\leq 2 a \\ 0 & \text{otherwise }\,, \end{cases}\end{split}\]

where \(F_1\) and \(F_2\) represent the foci of the ellipse, \(P\) is a generic point of coordinates \((\text{lon}, \text{lat})\), \(a\) is the major semiaxis of the ellipse and N is the model’s normalization, in units of \(\text{sr}^{-1}\).

The model is defined on the celestial sphere, with a normalization defined by:

\[\int_{4\pi}\phi(\text{lon}, \text{lat}) \,d\Omega = 1\,.\]

Parameters:

lon_0 : Longitude

\(\text{lon}_0\): lon coordinate for the center of the ellipse.

lat_0 : Latitude

\(\text{lat}_0\): lat coordinate for the center of the ellipse.

semi_major : Angle

\(a\): length of the major semiaxis, in angular units.

e : float

Eccentricity of the ellipse (\(0< e< 1\)).

theta : Angle

\(\theta\): Rotation angle of the major semiaxis. The rotation angle increases counter-clockwise from the North direction.

edge : Angle

Width of the edge. The width is defined as the range within the smooth edges of the model drops from 95% to 5% of its amplitude (see illustration for SkyDisk).

frame : {“galactic”, “icrs”}

Coordinate frame of lon_0 and lat_0.

Examples

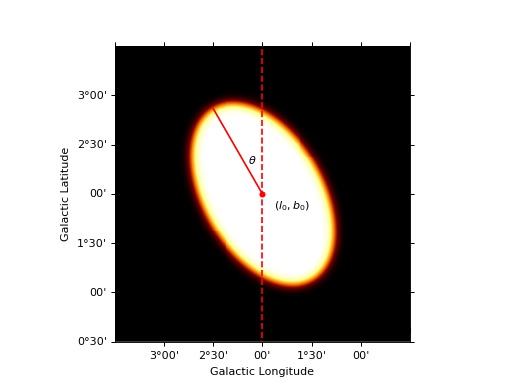
import numpy as np
import matplotlib.pyplot as plt
import astropy.units as u
from gammapy.image.models.core import SkyEllipse
from gammapy.maps import Map, WcsGeom

model = SkyEllipse("2 deg", "2 deg", "1 deg", 0.8, "30 deg", frame= "galactic")

m_geom = WcsGeom.create(binsz=0.01, width=(3, 3), skydir=(2, 2), coordsys="GAL", proj="AIT")
coords = m_geom.get_coord()
lon = coords.lon * u.deg
lat = coords.lat * u.deg
vals = model(lon, lat)
skymap = Map.from_geom(m_geom, data=vals.value)

_, ax, _ = skymap.smooth("0.05 deg").plot()

transform = ax.get_transform('galactic')
ax.scatter(2, 2, transform=transform, s=20, edgecolor='red', facecolor='red')
ax.text(1.7, 1.85, r"$(l_0, b_0)$", transform=transform, ha="center")
ax.plot([2, 2 + np.sin(np.pi / 6)], [2, 2 + np.cos(np.pi / 6)], color="r", transform=transform)
ax.vlines(x=2, color='r', linestyle='--', transform=transform, ymin=0, ymax=5)
ax.text(2.15, 2.3, r"$\theta$", transform=transform);

plt.show()

(png, hires.png, pdf)

Attributes Summary

e
evaluation_radius	Evaluation radius (Angle).
frame
lat_0
lon_0
parameters	Parameters (Parameters)
position	Spatial model center position
semi_major
theta

Methods Summary

__call__(self, lon, lat)	Call evaluate method
compute_norm(semi_major, e)	Compute the normalization factor.
copy(self)	A deep copy.
evaluate(self, lon, lat, lon_0, lat_0, …)	Evaluate the model (static function).
to_dict(self[, selection])

Attributes Documentation

e

evaluation_radius

Evaluation radius (Angle).

Set to the length of the semi-major axis.

frame

lat_0

lon_0

parameters

Parameters (Parameters)

position

Spatial model center position

semi_major

theta

Methods Documentation

__call__(self, lon, lat)

Call evaluate method

static compute_norm(semi_major, e)

Compute the normalization factor.

copy(self)

A deep copy.

evaluate(self, lon, lat, lon_0, lat_0, semi_major, e, theta, edge)

Evaluate the model (static function).

to_dict(self, selection='all')