This is a fixed-text formatted version of a Jupyter notebook.

• Try online
• You can contribute with your own notebooks in this GitHub repository.
• Source files: hess.ipynb | hess.py

H.E.S.S. with Gammapy

This tutorial explains how to analyse H.E.S.S. data with Gammapy.

We will analyse four observation runs of the Crab nebula, which are part of the H.E.S.S. first public test data release. In this tutorial we will make an image and a spectrum. The light_curve.ipynb notbook contains an example how to make a light curve.

To do a 3D analysis, one needs to do a 3D background estimate. In background_model.ipynb we have started to make a background model, and in this notebook we have a first look at a 3D analysis. But the results aren’t OK yet, the background model needs to be improved. In this analysis, we also don’t use the energy dispersion IRF yet, and we only analyse the data in the 1 TeV to 10 TeV range. The H.E.S.S. data was only released very recently, and 3D analysis in Gammapy is new. This tutorial will be improved soon.

%matplotlib inline
import matplotlib.pyplot as plt

import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from regions import CircleSkyRegion
from gammapy.data import DataStore
from gammapy.maps import Map, MapAxis, WcsGeom, WcsNDMap
from gammapy.cube import MapMaker, MapFit, PSFKernel
from gammapy.cube.models import SkyModel
from gammapy.spectrum.models import PowerLaw, ExponentialCutoffPowerLaw
from gammapy.image.models import SkyGaussian, SkyPointSource
from gammapy.detect import TSMapEstimator
from gammapy.scripts import SpectrumAnalysisIACT

Data access

To access the data, we use the DataStore, and we use the obs_table to select the Crab runs.

data_store = DataStore.from_file(
    "$GAMMAPY_DATA/hess-dl3-dr1/hess-dl3-dr3-with-background.fits.gz"
)
mask = data_store.obs_table["TARGET_NAME"] == "Crab"
obs_table = data_store.obs_table[mask]
observations = data_store.get_observations(obs_table["OBS_ID"])

# pos_crab = SkyCoord.from_name('Crab')
pos_crab = SkyCoord(83.633, 22.014, unit="deg")

Maps

Let’s make some 3D cubes, as well as 2D images.

For the energy, we make 5 bins from 1 TeV to 10 TeV.

energy_axis = MapAxis.from_edges(
    np.logspace(0, 1.0, 5), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
    skydir=(83.633, 22.014),
    binsz=0.02,
    width=(5, 5),
    coordsys="CEL",
    proj="TAN",
    axes=[energy_axis],
)

%%time
maker = MapMaker(geom, offset_max="2.5 deg")
maps = maker.run(observations)
images = maker.make_images()

CPU times: user 15.1 s, sys: 329 ms, total: 15.4 s
Wall time: 4 s

maps.keys()

dict_keys(['counts', 'exposure', 'background'])

images["counts"].smooth(3).plot(stretch="sqrt", vmax=2);

PSF

Compute the mean PSF for these observations at the Crab position.

from gammapy.irf import make_mean_psf

table_psf = make_mean_psf(observations, pos_crab)

/Users/deil/software/anaconda3/envs/gammapy-dev/lib/python3.7/site-packages/astropy/units/quantity.py:639: RuntimeWarning: invalid value encountered in true_divide
  result = super().__array_ufunc__(function, method, *arrays, **kwargs)

psf_kernel = PSFKernel.from_table_psf(table_psf, geom, max_radius="0.3 deg")
psf_kernel_array = psf_kernel.psf_kernel_map.sum_over_axes().data
# psf_kernel.psf_kernel_map.slice_by_idx({'energy': 0}).plot()
# plt.imshow(psf_kernel_array)

Map fit

Let’s fit this source assuming a Gaussian spatial shape and a power-law spectral shape

spatial_model = SkyPointSource(lon_0="83.6 deg", lat_0="22.0 deg")
spectral_model = PowerLaw(
    index=2.6, amplitude="5e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)
model = SkyModel(spatial_model=spatial_model, spectral_model=spectral_model)

%%time
fit = MapFit(
    model=model,
    counts=maps["counts"],
    exposure=maps["exposure"],
    background=maps["background"],
    psf=psf_kernel,
)
result = fit.run()
print(result)
print(result.model.parameters.to_table())

FitResult

        backend    : minuit
        method     : minuit
        success    : True
        nfev       : 116
        total stat : 67023.63
        message    : Optimization terminated successfully.

   name     value     error        unit      min max frozen
--------- --------- --------- -------------- --- --- ------
    lon_0 8.362e+01 2.703e-03            deg nan nan  False
    lat_0 2.203e+01 2.426e-03            deg nan nan  False
    index 2.616e+00 8.089e-02                nan nan  False
amplitude 6.012e-11 4.381e-12 cm-2 s-1 TeV-1 nan nan  False
reference 1.000e+00 0.000e+00            TeV nan nan   True
CPU times: user 7.82 s, sys: 71.2 ms, total: 7.89 s
Wall time: 2.01 s

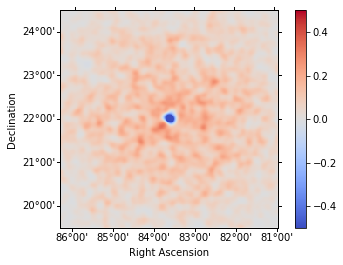
Residual image

We compute a residual image as residual = counts - model. Note that this is counts per pixel and our pixel size is 0.02 deg. Smoothing is counts-preserving. The residual image shows that currently both the source and the background modeling isn’t very good. The background model is underestimated (so residual is positive), and the source model is overestimated.

npred = fit.evaluator.compute_npred()
residual = Map.from_geom(maps["counts"].geom)
residual.data = maps["counts"].data - npred

residual.sum_over_axes().smooth(3).plot(
    cmap="coolwarm", vmin=-0.5, vmax=0.5, add_cbar=True
);

Spectrum

We could try to improve the background modeling and spatial model of the source. But let’s instead turn to one of the classic IACT analysis techniques: use a circular on region and reflected regions for background estimation, and derive a spectrum for the source without having to assume a spatial model, or without needing a 3D background model.

%%time
on_region = CircleSkyRegion(pos_crab, 0.11 * u.deg)
exclusion_mask = images["counts"].copy()
exclusion_mask.data = np.ones_like(exclusion_mask.data, dtype=bool)

model = PowerLaw(
    index=2.6, amplitude="5e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)

config = {
    "outdir": ".",
    "background": {"on_region": on_region, "exclusion_mask": exclusion_mask},
    "extraction": {"containment_correction": True},
    "fit": {"model": model, "fit_range": [1, 10] * u.TeV},
    "fp_binning": np.logspace(0, 1, 7) * u.TeV,
}
analysis = SpectrumAnalysisIACT(observations=observations, config=config)
analysis.run()

CPU times: user 10.8 s, sys: 63.5 ms, total: 10.9 s
Wall time: 5.81 s

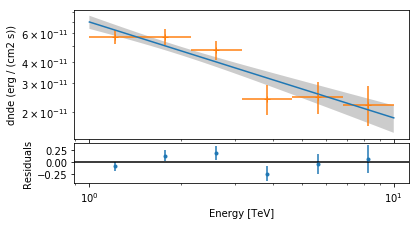
print(analysis.fit.result[0])

Fit result info
---------------
Model: PowerLaw

Parameters:

           name     value     error        unit      min max frozen
        --------- --------- --------- -------------- --- --- ------
            index 2.577e+00 1.078e-01                nan nan  False
        amplitude 4.354e-11 3.959e-12 cm-2 s-1 TeV-1 nan nan  False
        reference 1.000e+00 0.000e+00            TeV nan nan   True

Covariance:

           name     index   amplitude reference
        --------- --------- --------- ---------
            index 1.163e-02 3.288e-13 0.000e+00
        amplitude 3.288e-13 1.567e-23 0.000e+00
        reference 0.000e+00 0.000e+00 0.000e+00

Statistic: 27.477 (wstat)
Fit Range: [ 1. 10.] TeV

opts = {
    "energy_range": analysis.fit.fit_range,
    "energy_power": 2,
    "flux_unit": "erg-1 cm-2 s-1",
}
axes = analysis.spectrum_result.plot(**opts)

Again: please note that this tutorial notebook was put together quickly, the results obtained here are very preliminary. We will work on Gammapy and the analysis of data from the H.E.S.S. test release and update this tutorial soon.

Exercises

• Try analysing another source, e.g. MSH 15-52.
• Try another model, e.g. a Gaussian spatial shape or exponential cutoff power-law spectrum.