This is a fixed-text formatted version of a Jupyter notebook.
- Try online
- You can contribute with your own notebooks in this GitHub repository.
- Source files: intro_maps.ipynb | intro_maps.py
Gammapy Maps¶
Gammapy Maps Illustration
Introduction¶
The gammapy.maps submodule contains classes for
representing sky images with an arbitrary number of non-spatial
dimensions such as energy, time, event class or any possible
user-defined dimension (illustrated in the image above). The main
Map data structure features a uniform API for
WCS as well as
HEALPix based images. The
API also generalizes simple image based operations such as smoothing,
interpolation and reprojection to the arbitrary extra dimensions and
makes working with (2 + N)-dimensional hypercubes as easy as working
with a simple 2D image. Further information is also provided on the
gammpy.maps docs page.
In the following introduction we will learn all the basics of working with WCS based maps. HEALPix based maps will be covered in a future tutorial. We will cover the following topics in order:
- Creating WCS Maps
- Accessing and Modifying Data
- Reading and Writing
- Visualizing and Plotting
- Reprojecting, Interpolating and Miscellaneous
Make sure you have worked through he First Steps with
Gammapy and Astropy
Introduction notebooks, because a solid
knowledge about working with SkyCoords and Quantity objects as
well as Numpy is required for this tutorial.
Note: This notebook is rather lengthy, but getting to know the
Map data structure in detail is essential for working with
Gammapy and will allow you to fulfill complex analysis tasks with
very few and simple code in future!
0. Setup¶
In [1]:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import os
In [2]:
from astropy import units as u
from astropy.io import fits
from astropy.table import Table
from astropy.coordinates import SkyCoord
from gammapy.maps import Map, MapAxis, WcsGeom
1. Creating WCS Maps¶
1.1 Using Factory Methods¶
Maps are most easily created using the Map.create() factory method:
In [3]:
m_allsky = Map.create()
Calling Map.create() without any further arguments creates by
default an allsky WCS map using a CAR projection, ICRS coordinates and a
pixel size of 1 deg. This can be easily checked by printing the
.geom attribute of the map:
In [4]:
print(m_allsky.geom)
WcsGeom
axes : lon, lat
shape : (3600, 1800)
ndim : 2
coordsys : CEL
projection : CAR
center : 0.0 deg, 0.0 deg
width : 360.0 x 180.0 deg
The .geom attribute is a MapGeom object, that defines the basic
geometry of the map, such as size of the pixels, width and height of the
image, coordinate system etc., but we will learn more about this object
later.
Besides the .geom attribute the map has also a .data attribute,
which is just a plain numpy.ndarray and stores the data associated
with this map:
In [5]:
m_allsky.data
Out[5]:
array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]], dtype=float32)
By default maps are filled with zeros.
Here is a second example that creates a WCS map centered on the Galactic center and now uses Galactic coordinates:
In [6]:
skydir = SkyCoord(0, 0, frame="galactic", unit="deg")
m_gc = Map.create(
binsz=0.02, width=(10, 5), skydir=skydir, coordsys="GAL", proj="TAN"
)
print(m_gc.geom)
WcsGeom
axes : lon, lat
shape : (500, 250)
ndim : 2
coordsys : GAL
projection : TAN
center : 0.0 deg, 0.0 deg
width : 10.0 x 5.0 deg
In addition we have defined a TAN projection, a pixel size of 0.02
deg and a width of the map of 10 deg x 5 deg. The width argument
also takes scalar value instead of a tuple, which is interpreted as both
the width and height of the map, so that a quadratic map is created.
1.2 Creating from a Map Geometry¶
As we have seen in the first examples, the Map object couples the
data (stored as a numpy.ndarray) with a MapGeom object. The
MapGeom object can be seen as a generalization of an
astropy.wcs.WCS object, providing the information on how the data
maps to physical coordinate systems. In some cases e.g. when creating
many maps with the same WCS geometry it can be advantegeous to first
create the map geometry independent of the map object itsself:
In [7]:
wcs_geom = WcsGeom.create(
binsz=0.02, width=(10, 5), skydir=(0, 0), coordsys="GAL"
)
And then create the map objects from the wcs_geom geometry
specification:
In [8]:
maps = {}
for name in ["counts", "background"]:
maps[name] = Map.from_geom(wcs_geom)
The MapGeom object also has a few helpful methods. E.g. we can check
whether a given position on the sky is contained in the map geometry:
In [9]:
# define the position of the Galactic center and anti-center
positions = SkyCoord([0, 180], [0, 0], frame="galactic", unit="deg")
wcs_geom.contains(positions)
Out[9]:
array([ True, False])
Or get the image center of the map:
In [10]:
wcs_geom.center_skydir
Out[10]:
<SkyCoord (Galactic): (l, b) in deg
(0., 0.)>
Or we can also retrieve the solid angle per pixel of the map:
In [11]:
wcs_geom.solid_angle()
Out[11]:
1.3 Adding Non-Spatial Axes¶
In many analysis scenarios we would like to add extra dimension to the
maps to study e.g. energy or time dependency of the data. Those
non-spatial dimensions are handled with the MapAxis object. Let us
first define an energy axis, with 4 bins:
In [12]:
energy_axis = MapAxis.from_bounds(
1, 100, nbin=4, unit="TeV", name="energy", interp="log"
)
print(energy_axis)
MapAxis
name : energy
unit : 'TeV'
nbins : 4
node type : edges
edges min : 1.0e+00 TeV
edges max : 1.0e+02 TeV
interp : log
Where interp='log' specifies that a logarithmic spacing is used
between the bins, equivalent to np.logspace(0, 2, 4). This
MapAxis object we can now pass to Map.create() using the
axes= argument:
In [13]:
m_cube = Map.create(
binsz=0.02, width=(10, 5), coordsys="GAL", axes=[energy_axis]
)
print(m_cube.geom)
WcsGeom
axes : lon, lat, energy
shape : (500, 250, 4)
ndim : 3
coordsys : GAL
projection : CAR
center : 0.0 deg, 0.0 deg
width : 10.0 x 5.0 deg
Now we see that besides lon and lat the map has an additional
axes named energy with 4 bins. The total dimension of the map is now
ndim=3.
We can also add further axes by passing a list of MapAxis objects.
To demonstrate this we create a time axis with linearly spaced bins and
pass both axes to Map.create():
In [14]:
time_axis = MapAxis.from_bounds(
0, 24, nbin=24, unit="hour", name="time", interp="lin"
)
m_4d = Map.create(
binsz=0.02, width=(10, 5), coordsys="GAL", axes=[energy_axis, time_axis]
)
print(m_4d.geom)
WcsGeom
axes : lon, lat, energy, time
shape : (500, 250, 4, 24)
ndim : 4
coordsys : GAL
projection : CAR
center : 0.0 deg, 0.0 deg
width : 10.0 x 5.0 deg
The MapAxis object internally stores the coordinates or “position
values” associated with every map axis bin or “node”. We distinguish
between two node types: edges and center. The node type
edges(which is also the default) specifies that the data
associated with this axis is integrated between the edges of the bin
(e.g. counts data). The node type center specifies that the data is
given at the center of the bin (e.g. exposure or differential fluxes).
The edges of the bins can be checked with .edges attribute:
In [15]:
energy_axis.edges
Out[15]:
array([ 1. , 3.16227766, 10. , 31.6227766 ,
100. ])
The numbers are given in the units we specified above, which can be checked again with:
In [16]:
energy_axis.unit
Out[16]:
The centers of the axis bins can be checked with the .center
attribute:
In [17]:
energy_axis.center
Out[17]:
array([ 1.77827941, 5.62341325, 17.7827941 , 56.23413252])
2. Accessing and Modifying Data¶
2.1 Accessing Map Data Values¶
All map objects have a set of accessor methods, which can be used to
access or update the contents of the map irrespective of its underlying
representation. Those accessor methods accept as their first argument a
coordinate tuple containing scalars, list, or numpy.ndarray
with one tuple element for each dimension. Some methods additionally
accept a dict or MapCoord argument, of which both allow to
assign coordinates by axis name.
Let us first begin with the .get_by_idx() method, that accepts a
tuple of indices. The order of the indices corresponds to the axis order
of the map:
In [18]:
m_gc.get_by_idx((50, 30))
Out[18]:
array([0.], dtype=float32)
Important: Gammapy uses a reversed index order in the map API with the longitude axes first. To achieve the same by directly indexing into the numpy array we have to call:
In [19]:
m_gc.data[([30], [50])]
Out[19]:
array([0.], dtype=float32)
To check the order of the axes you can always print the .geom
attribute:
In [20]:
print(m_gc.geom)
WcsGeom
axes : lon, lat
shape : (500, 250)
ndim : 2
coordsys : GAL
projection : TAN
center : 0.0 deg, 0.0 deg
width : 10.0 x 5.0 deg
To access values directly by sky coordinates we can use the
.get_by_coord() method. This time we pass in a dict, specifying
the axes names corresponding to the given coordinates:
In [21]:
m_gc.get_by_coord({"lon": [0, 180], "lat": [0, 0]})
Out[21]:
array([ 0., nan], dtype=float32)
The units of the coordinates are assumed to be in degrees in the
coordinate system used by the map. If the coordinates do not correspond
to the exact pixel center, the value of the nearest pixel center will be
returned. For positions outside the map geometry np.nan is returned.
The coordinate or idx arrays follow normal Numpy broadcasting rules. So the following works as expected:
In [22]:
lons = np.linspace(-4, 4, 10)
m_gc.get_by_coord({"lon": lons, "lat": 0})
Out[22]:
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)
Or as an even more advanced example, we can provide lats as column
vector and broadcasting to a 2D result array will be applied:
In [23]:
lons = np.linspace(-4, 4, 8)
lats = np.linspace(-4, 4, 8).reshape(-1, 1)
m_gc.get_by_coord({"lon": lons, "lat": lats})
Out[23]:
array([[nan, nan, nan, nan, nan, nan, nan, nan],
[nan, nan, nan, nan, nan, nan, nan, nan],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[nan, nan, nan, nan, nan, nan, nan, nan],
[nan, nan, nan, nan, nan, nan, nan, nan]], dtype=float32)
2.2 Modifying Map Data Values¶
To modify and set map data values the Map object features as well a
.set_by_idx() method:
In [24]:
m_cube.set_by_idx(idx=(10, 20, 3), vals=42)
In [25]:
m_cube.get_by_idx((10, 20, 3))
Out[25]:
array([42.], dtype=float32)
Of course there is also a .set_by_coord() method, which allows to
set map data values in physical coordinates.
In [26]:
m_cube.set_by_coord({"lon": 0, "lat": 0, "energy": 2 * u.TeV}, vals=42)
Again the lon and lat values are assumed to be given in degrees
in the coordinate system used by the map. For the energy axis, the unit
is the one specified on the axis (use m_cube.geom.axes[0].unit to
check if needed…)
All .xxx_by_coord() methods accept SkyCoord objects as well. In
this case we have to use the skycoord keyword instead of lon and
lat:
In [27]:
skycoords = SkyCoord([1.2, 3.4], [-0.5, 1.1], frame="galactic", unit="deg")
m_cube.set_by_coord({"skycoord": skycoords, "energy": 2 * u.TeV}, vals=42)
2.3 Indexing and Slicing Sub-Maps¶
When you have worked with Numpy arrays in the past you are probably
familiar with the concept of indexing and slicing into data arrays. To
support slicing of non-spatial axes of Map objects, the Map
object has a .slice_by_idx() method, which allows to extract
sub-maps from a larger map.
The following example demonstrates how to get the map at the energy bin number 3:
In [28]:
m_sub = m_cube.slice_by_idx({"energy": 3})
print(m_sub)
WcsNDMap
geom : WcsGeom
axes : lon, lat
shape : (500, 250)
ndim : 2
unit : ''
dtype : float32
Note that the returned object is again a Map with updated axes
information. In this case, because we extracted only a single image, the
energy axes is dropped from the map.
To extract a sub-cube with a sliced energy axes we can use a normal
slice() object:
In [29]:
m_sub = m_cube.slice_by_idx({"energy": slice(1, 3)})
print(m_sub)
WcsNDMap
geom : WcsGeom
axes : lon, lat, energy
shape : (500, 250, 2)
ndim : 3
unit : ''
dtype : float32
Note that the returned object is also a Map object, but this time
with updated energy axis specification.
Slicing of multiple dimensions is supported by adding further entries to
the dict passed to .slice_by_idx()
In [30]:
m_sub = m_4d.slice_by_idx({"energy": slice(1, 3), "time": slice(4, 10)})
print(m_sub)
WcsNDMap
geom : WcsGeom
axes : lon, lat, energy, time
shape : (500, 250, 2, 6)
ndim : 4
unit : ''
dtype : float32
For convenience there is also a .get_image_by_coord() method which
allows to access image planes at given non-spatial physical coordinates.
This method also supports Quantity objects:
In [31]:
image = m_4d.get_image_by_coord({"energy": 4 * u.TeV, "time": 5 * u.h})
print(image.geom)
WcsGeom
axes : lon, lat
shape : (500, 250)
ndim : 2
coordsys : GAL
projection : CAR
center : 0.0 deg, 0.0 deg
width : 10.0 x 5.0 deg
3. Reading and Writing¶
Gammapy Map objects are serialized using the Flexible Image
Transport Format (FITS). Depending on the pixelisation scheme (HEALPix
or WCS) and presence of non-spatial dimensions the actual convention to
write the FITS file is different. By default Gammpy uses a generic
convention named gadf, which will support WCS and HEALPix formats as
well as an arbitrary number of non-spatial axes. The convention is
documented in detail on the Gamma Astro Data
Formats
page.
Other conventions required by specific software (e.g. the Fermi Science Tools) are supported as well. At the moment those are the following
fgst-ccube: Fermi counts cube format.fgst-ltcube: Fermi livetime cube format.fgst-bexpcube: Fermi exposure cube formatfgst-template: Fermi Galactic diffuse and source template format.fgst-srcmapandfgst-srcmap-sparse: Fermi source map and sparse source map format.
The conventions listed above only support an additional energy axis.
3.1 Reading Maps¶
Reading FITS files is mainly exposed via the Map.read() method.Let
us take a look at a first example:
In [32]:
filename = "$GAMMAPY_DATA/fermi_2fhl/fermi_2fhl_gc.fits.gz"
m_2fhl_gc = Map.read(filename)
print(m_2fhl_gc)
WcsNDMap
geom : WcsGeom
axes : lon, lat
shape : (320, 180)
ndim : 2
unit : ''
dtype : >f8
By default Map.read() will try to find the first valid data hdu in
the filename and read the data from there. If mutliple HDUs are present
in the FITS file, the desired one can be chosen with the additional
hdu= argument:
In [33]:
m_2fhl_gc = Map.read(filename, hdu="background")
print(m_2fhl_gc)
WcsNDMap
geom : WcsGeom
axes : lon, lat
shape : (320, 180)
ndim : 2
unit : ''
dtype : >f8
In rare cases e.g. when the FITS file is not valid or meta data is
missing from the header it can be necessary to modify the header of a
certain HDU before creating the Map object. In this case we can use
astropy.io.fits directly to read the FITS file:
In [34]:
filename = os.environ["GAMMAPY_DATA"] + "/fermi_survey/all.fits.gz"
hdulist = fits.open(filename)
hdulist.info()
Filename: /Users/deil/work/gammapy-tutorials/datasets/fermi_survey/all.fits.gz
No. Name Ver Type Cards Dimensions Format
0 COUNTS 1 PrimaryHDU 84 (2001, 101) int32
1 BACKGROUND 1 ImageHDU 85 (2001, 101) float64
2 EXPOSURE 1 ImageHDU 85 (2001, 101) float32
And then modify the header keyword and use Map.from_hdulist() to
create the Map object after:
In [35]:
hdulist["exposure"].header["BUNIT"] = "cm2 s"
Map.from_hdulist(hdulist=hdulist, hdu="exposure")
Out[35]:
WcsNDMap
geom : WcsGeom
axes : lon, lat
shape : (2001, 101)
ndim : 2
unit : 'cm2 s'
dtype : >f4
3.2 Writing Maps¶
Writing FITS files is mainoy exposure via the Map.write() method.
Here is a first example:
In [36]:
m_cube.write("example_cube.fits", overwrite=True)
By default Gammapy does not overwrite files. In this example we set
overwrite=True in case the cell gets executed multiple times. Now we
can read back the cube from disk using Map.read():
In [37]:
m_cube = Map.read("example_cube.fits")
print(m_cube)
WcsNDMap
geom : WcsGeom
axes : lon, lat, energy
shape : (500, 250, 4)
ndim : 3
unit : ''
dtype : >f4
We can also choose a different FITS convention to write the example cube in a format compatible to the Fermi Galactic diffuse background model:
In [38]:
m_cube.write("example_cube_fgst.fits", conv="fgst-template", overwrite=True)
To understand a little bit better the generic gadf convention we use
Map.to_hdulist() to generate a list of FITS HDUs first:
In [39]:
hdulist = m_4d.to_hdulist(conv="gadf")
hdulist.info()
Filename: (No file associated with this HDUList)
No. Name Ver Type Cards Dimensions Format
0 PRIMARY 1 PrimaryHDU 29 (500, 250, 4, 24) float32
1 PRIMARY_BANDS 1 BinTableHDU 33 96R x 7C ['I', 'E', 'E', 'E', 'E', 'E', 'E']
As we can see the HDUList object contains to HDUs. The first one
named PRIMARY contains the data array with shape corresponding to
our data and the WCS information stored in the header:
In [40]:
hdulist["PRIMARY"].header
Out[40]:
SIMPLE = T / conforms to FITS standard
BITPIX = -32 / array data type
NAXIS = 4 / number of array dimensions
NAXIS1 = 500
NAXIS2 = 250
NAXIS3 = 4
NAXIS4 = 24
EXTEND = T
WCSAXES = 2 / Number of coordinate axes
CRPIX1 = 250.5 / Pixel coordinate of reference point
CRPIX2 = 125.5 / Pixel coordinate of reference point
CDELT1 = -0.02 / [deg] Coordinate increment at reference point
CDELT2 = 0.02 / [deg] Coordinate increment at reference point
CUNIT1 = 'deg' / Units of coordinate increment and value
CUNIT2 = 'deg' / Units of coordinate increment and value
CTYPE1 = 'GLON-CAR' / galactic longitude, plate caree projection
CTYPE2 = 'GLAT-CAR' / galactic latitude, plate caree projection
CRVAL1 = 0.0 / [deg] Coordinate value at reference point
CRVAL2 = 0.0 / [deg] Coordinate value at reference point
LONPOLE = 0.0 / [deg] Native longitude of celestial pole
LATPOLE = 90.0 / [deg] Native latitude of celestial pole
AXCOLS1 = 'E_MIN,E_MAX'
INTERP1 = 'log '
AXCOLS2 = 'TIME_MIN,TIME_MAX'
INTERP2 = 'lin '
WCSSHAPE= '(500,250,4,24)'
BANDSHDU= 'PRIMARY_BANDS'
META = '{} '
BUNIT = ''
The second HDU is a BinTableHDU named PRIMARY_BANDS contains the
information on the non-spatial axes such as name, order, unit, min, max
and center values of the axis bins. We use an astropy.table.Table to
show the information:
In [41]:
Table.read(hdulist["PRIMARY_BANDS"])
Out[41]:
| CHANNEL | ENERGY | E_MIN | E_MAX | TIME | TIME_MIN | TIME_MAX |
|---|---|---|---|---|---|---|
| TeV | TeV | TeV | h | h | h | |
| int16 | float32 | float32 | float32 | float32 | float32 | float32 |
| 0 | 1.7782794 | 1.0 | 3.1622777 | 0.5 | 0.0 | 1.0 |
| 1 | 5.623413 | 3.1622777 | 10.0 | 0.5 | 0.0 | 1.0 |
| 2 | 17.782795 | 10.0 | 31.622776 | 0.5 | 0.0 | 1.0 |
| 3 | 56.23413 | 31.622776 | 100.0 | 0.5 | 0.0 | 1.0 |
| 4 | 1.7782794 | 1.0 | 3.1622777 | 1.5 | 1.0 | 2.0 |
| 5 | 5.623413 | 3.1622777 | 10.0 | 1.5 | 1.0 | 2.0 |
| 6 | 17.782795 | 10.0 | 31.622776 | 1.5 | 1.0 | 2.0 |
| 7 | 56.23413 | 31.622776 | 100.0 | 1.5 | 1.0 | 2.0 |
| 8 | 1.7782794 | 1.0 | 3.1622777 | 2.5 | 2.0 | 3.0 |
| ... | ... | ... | ... | ... | ... | ... |
| 86 | 17.782795 | 10.0 | 31.622776 | 21.5 | 21.0 | 22.0 |
| 87 | 56.23413 | 31.622776 | 100.0 | 21.5 | 21.0 | 22.0 |
| 88 | 1.7782794 | 1.0 | 3.1622777 | 22.5 | 22.0 | 23.0 |
| 89 | 5.623413 | 3.1622777 | 10.0 | 22.5 | 22.0 | 23.0 |
| 90 | 17.782795 | 10.0 | 31.622776 | 22.5 | 22.0 | 23.0 |
| 91 | 56.23413 | 31.622776 | 100.0 | 22.5 | 22.0 | 23.0 |
| 92 | 1.7782794 | 1.0 | 3.1622777 | 23.5 | 23.0 | 24.0 |
| 93 | 5.623413 | 3.1622777 | 10.0 | 23.5 | 23.0 | 24.0 |
| 94 | 17.782795 | 10.0 | 31.622776 | 23.5 | 23.0 | 24.0 |
| 95 | 56.23413 | 31.622776 | 100.0 | 23.5 | 23.0 | 24.0 |
4. Visualizing and Plotting¶
4.1 Plotting¶
For debugging and inspecting the map data it is useful to plot ot visualize the images planes contained in the map.
In [42]:
filename = "$GAMMAPY_DATA/fermi_2fhl/fermi_2fhl_gc.fits.gz"
m_2fhl_gc = Map.read(filename, hdu="counts")
After reading the map we can now plot it on the screen by calling the
.plot() method:
In [43]:
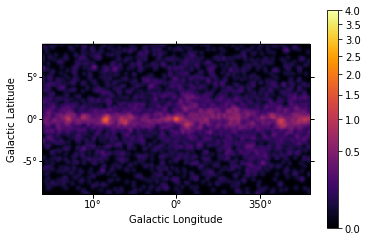
m_2fhl_gc.plot();

We can easily improve the plot by calling Map.smooth() first and
providing additional arguments to .plot(). Most of them are passed
further to
plt.imshow():
In [44]:
smoothed = m_2fhl_gc.smooth(width=0.2 * u.deg, kernel="gauss")
smoothed.plot(stretch="sqrt", add_cbar=True, vmax=4, cmap="inferno");
We can use the plt.rc_context() context manager to further tweak the plot by adapting the figure and font size:
In [45]:
rc_params = {"figure.figsize": (12, 5.4), "font.size": 12}
with plt.rc_context(rc=rc_params):
smoothed = m_2fhl_gc.smooth(width=0.2 * u.deg, kernel="gauss")
smoothed.plot(stretch="sqrt", add_cbar=True, vmax=4);

4.2 Interactive Plotting¶
For maps with non-spatial dimensions the Map object features an
interactive plotting method, that works in jupyter notebooks only
(Note: it requires the package ipywidgets to be installed). We
first read a small example cutout from the Fermi Galactic diffuse model
and display the data cube by calling .plot_interactive():
In [46]:
filename = "$GAMMAPY_DATA/fermi_3fhl/gll_iem_v06_cutout.fits"
m_iem_gc = Map.read(filename)
rc_params = {
"figure.figsize": (12, 5.4),
"font.size": 12,
"axes.formatter.limits": (2, -2),
}
m_iem_gc.plot_interactive(add_cbar=True, stretch="sqrt", rc_params=rc_params)
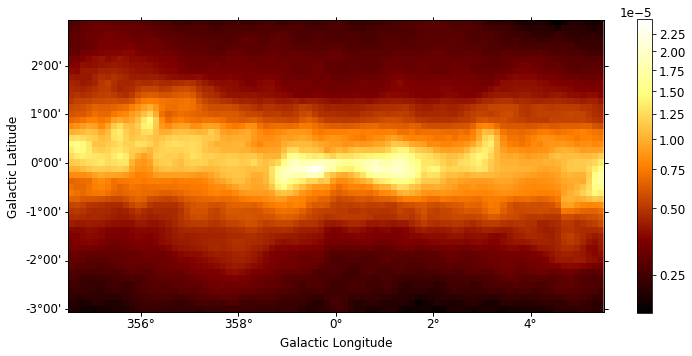
Now you can use the interactive slider to select an energy range and the
corresponding image is diplayed on the screen. You can also use the
radio buttons to select your preferred image stretching. We have passed
additional keywords using the rc_params argument to improve the
figure and font size. Those keywords are directly passed to the
plt.rc_context()
context manager.
5. Reprojecting, Interpolating and Miscellaneous¶
5.1 Reprojecting to Different Map Geometries¶
The example map m_iem_gc is given in Galactic coordinates:
In [47]:
print(m_iem_gc.geom)
WcsGeom
axes : lon, lat, energy
shape : (88, 48, 30)
ndim : 3
coordsys : GAL
projection : CAR
center : 0.0 deg, -0.1 deg
width : 11.0 x 6.0 deg
As an example we will now extract the image at ~10 GeV and reproject
it to ICRS coordinates. For this we first define the target map WCS
geometry. As .reproject() only applies to the spatial axes, we do
not have to specify any additional non-spatial axes:
In [48]:
skydir = SkyCoord(266.4, -28.9, frame="icrs", unit="deg")
wcs_geom_cel = WcsGeom.create(
skydir=skydir, binsz=0.1, coordsys="CEL", width=(8, 4)
)
Then we extract the image at ~10 GeV, reproject to the target
geometry and plot the result:
In [49]:
m_iem = m_iem_gc.get_image_by_coord({"energy": 10 * u.GeV})
m_iem_cel = m_iem.reproject(wcs_geom_cel)
m_iem_cel.plot(add_cbar=True, vmin=0, vmax=2.5e-9)
Out[49]:
(<Figure size 432x288 with 2 Axes>,
<matplotlib.axes._subplots.WCSAxesSubplot at 0x1c236c0208>,
<matplotlib.colorbar.Colorbar at 0x1c1ee38da0>)

5.2 Interpolating Map Values¶
While for the reprojection example above we used
.get_image_by_coord() to extract the closest image to ~10 GeV,
we can use the more general method .interp_by_coord() to interpolate
in the energy axis as well. For this we first define again the target
map geometry:
In [50]:
m_iem_10GeV = Map.from_geom(wcs_geom_cel)
coords = m_iem_10GeV.geom.get_coord()
m_iem_10GeV.data = m_iem_gc.interp_by_coord(
{"skycoord": coords.skycoord, "energy": 10 * u.GeV},
interp="linear",
fill_value=np.nan,
)
m_iem_10GeV.plot(add_cbar=True, vmin=0, vmax=2.5e-9);

5.3 Making Cutouts¶
The WCSNDMap objects features a .cutout() method, which allows
you to cut out a smaller part of a larger map. This can be useful,
e.g. when working with allsky diffuse maps. Here is an example:
In [51]:
position = SkyCoord(0, 0, frame="galactic", unit="deg")
m_iem_cutout = m_iem_gc.cutout(position=position, width=(4 * u.deg, 2 * u.deg))
rc_params = {
"figure.figsize": (12, 5.4),
"font.size": 12,
"axes.formatter.limits": (2, -2),
}
m_iem_cutout.plot_interactive(
add_cbar=True, rc_params=rc_params, stretch="linear"
)

The returned object is again a Map object with udpated WCS
information and data size. As one can see the cutout is automatically
applied to all the non-spatial axes as well. The cutout width is given
in the order of (lon, lat) and can be specified with units that will
be handled correctly.
In [52]: