This is a fixed-text formatted version of a Jupyter notebook.

Flux point fitting in Gammapy

Introduction

In this tutorial we’re going to learn how to fit spectral models to combined Fermi-LAT and IACT flux points.

The central class we’re going to use for this example analysis is:

In addition we will work with the following data classes:

And the following spectral model classes:

Setup

Let us start with the usual IPython notebook and Python imports:

In [1]:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

In [2]:

from astropy import units as u
from gammapy.spectrum.models import (
    PowerLaw,
    ExponentialCutoffPowerLaw,
    LogParabola,
)
from gammapy.spectrum import FluxPointFit, FluxPoints
from gammapy.catalog import (
    SourceCatalog3FGL,
    SourceCatalogGammaCat,
    SourceCatalog3FHL,
)

Load spectral points

For this analysis we choose to work with the source ‘HESS J1507-622’ and the associated Fermi-LAT sources ‘3FGL J1506.6-6219’ and ‘3FHL J1507.9-6228e’. We load the source catalogs, and then access source of interest by name:

In [3]:

fermi_3fgl = SourceCatalog3FGL()
fermi_3fhl = SourceCatalog3FHL()
gammacat = SourceCatalogGammaCat()

In [4]:

source_gammacat = gammacat["HESS J1507-622"]
source_fermi_3fgl = fermi_3fgl["3FGL J1506.6-6219"]
source_fermi_3fhl = fermi_3fhl["3FHL J1507.9-6228e"]

The corresponding flux points data can be accessed with .flux_points attribute:

In [5]:

flux_points_gammacat = source_gammacat.flux_points
flux_points_gammacat.table

Out[5]:
Table length=6
e_refdndednde_errndnde_errp
TeV1 / (cm2 s TeV)1 / (cm2 s TeV)1 / (cm2 s TeV)
float32float32float32float32
0.86090042.29119e-128.705427e-138.955021e-13
1.5615126.981717e-132.203541e-132.304066e-13
2.7637531.690615e-136.758698e-147.188384e-14
4.8915977.729249e-142.401318e-142.607487e-14
9.9885841.032534e-145.063147e-155.641954e-15
27.040357.449867e-165.72089e-167.259987e-16

In the Fermi-LAT catalogs, integral flux points are given. Currently the flux point fitter only works with differential flux points, so we apply the conversion here.

In [6]:

flux_points_3fgl = source_fermi_3fgl.flux_points.to_sed_type(
    sed_type="dnde", model=source_fermi_3fgl.spectral_model
)
flux_points_3fhl = source_fermi_3fhl.flux_points.to_sed_type(
    sed_type="dnde", model=source_fermi_3fhl.spectral_model
)

Finally we stack the flux points into a single FluxPoints object and drop the upper limit values, because currently we can’t handle them in the fit:

In [7]:

# stack flux point tables
flux_points = FluxPoints.stack(
    [flux_points_gammacat, flux_points_3fhl, flux_points_3fgl]
)

# drop the flux upper limit values
flux_points = flux_points.drop_ul()

Power Law Fit

First we start with fitting a simple power law.

In [8]:

pwl = PowerLaw(index=2, amplitude="1e-12 cm-2 s-1 TeV-1", reference="1 TeV")

After creating the model we run the fit by passing the 'flux_points' and 'pwl' objects:

In [9]:

fitter = FluxPointFit(pwl, flux_points, stat="chi2assym")
result_pwl = fitter.run()

And print the result:

In [10]:

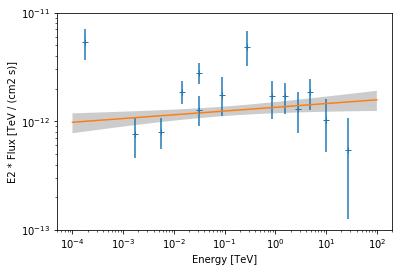
print(result_pwl.model)

PowerLaw

Parameters:

           name     value     error        unit      min max frozen
        --------- --------- --------- -------------- --- --- ------
            index 1.966e+00 2.651e-02                nan nan  False
        amplitude 1.345e-12 1.595e-13 cm-2 s-1 TeV-1 nan nan  False
        reference 1.000e+00 0.000e+00            TeV nan nan   True

Covariance:

           name     index    amplitude  reference
        --------- ---------- ---------- ---------
            index  7.029e-04 -2.230e-15 0.000e+00
        amplitude -2.230e-15  2.543e-26 0.000e+00
        reference  0.000e+00  0.000e+00 0.000e+00

Finally we plot the data points and the best fit model:

In [11]:

ax = flux_points.plot(energy_power=2)
result_pwl.model.plot(energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2)
result_pwl.model.plot_error(
    energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2
)
ax.set_ylim(1e-13, 1e-11);
../_images/notebooks_sed_fitting_gammacat_fermi_21_0.png

Exponential Cut-Off Powerlaw Fit

Next we fit an exponential cut-off power law to the data.

In [12]:

ecpl = ExponentialCutoffPowerLaw(
    index=2,
    amplitude="1e-12 cm-2 s-1 TeV-1",
    reference="1 TeV",
    lambda_="0.1 TeV-1",
)

We run the fitter again by passing the flux points and the ecpl model instance:

In [13]:

fitter = FluxPointFit(ecpl, flux_points, stat="chi2assym")
result_ecpl = fitter.run()
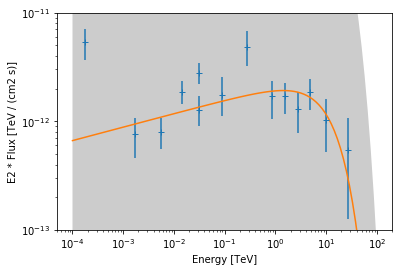
print(result_ecpl.model)

ExponentialCutoffPowerLaw

Parameters:

           name     value     error        unit      min max frozen
        --------- --------- --------- -------------- --- --- ------
            index 1.876e+00 4.517e-02                nan nan  False
        amplitude 2.077e-12 4.105e-13 cm-2 s-1 TeV-1 nan nan  False
        reference 1.000e+00 0.000e+00            TeV nan nan   True
          lambda_ 8.703e-02 5.699e-02          TeV-1 nan nan  False

Covariance:

           name     index    amplitude  reference  lambda_
        --------- ---------- ---------- --------- ----------
            index  2.041e-03 -1.506e-14 0.000e+00 -1.832e-03
        amplitude -1.506e-14  1.685e-25 0.000e+00  1.851e-14
        reference  0.000e+00  0.000e+00 0.000e+00  0.000e+00
          lambda_ -1.832e-03  1.851e-14 0.000e+00  3.248e-03

We plot the data and best fit model:

In [14]:

ax = flux_points.plot(energy_power=2)
result_ecpl.model.plot(energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2)
result_ecpl.model.plot_error(
    energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2
)
ax.set_ylim(1e-13, 1e-11)

Out[14]:

(1e-13, 1e-11)
../_images/notebooks_sed_fitting_gammacat_fermi_27_1.png

Log-Parabola Fit

Finally we try to fit a log-parabola model:

In [15]:

log_parabola = LogParabola(
    alpha=2, amplitude="1e-12 cm-2 s-1 TeV-1", reference="1 TeV", beta=0.1
)

In [16]:

fitter = FluxPointFit(log_parabola, flux_points, stat="chi2assym")
result_log_parabola = fitter.run()
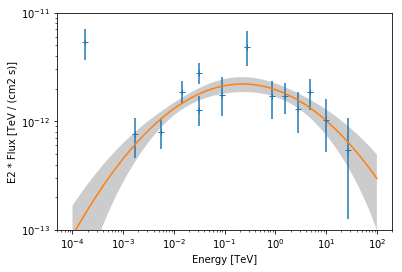
print(result_log_parabola.model)

LogParabola

Parameters:

           name     value     error        unit      min max frozen
        --------- --------- --------- -------------- --- --- ------
        amplitude 1.953e-12 2.799e-13 cm-2 s-1 TeV-1 nan nan  False
        reference 1.000e+00 0.000e+00            TeV nan nan   True
            alpha 2.161e+00 7.412e-02                nan nan  False
             beta 5.385e-02 1.763e-02                nan nan  False

Covariance:

           name   amplitude reference   alpha      beta
        --------- --------- --------- --------- ---------
        amplitude 7.835e-26 0.000e+00 1.753e-15 2.184e-15
        reference 0.000e+00 0.000e+00 0.000e+00 0.000e+00
            alpha 1.753e-15 0.000e+00 5.494e-03 1.127e-03
             beta 2.184e-15 0.000e+00 1.127e-03 3.109e-04

In [17]:

ax = flux_points.plot(energy_power=2)
result_log_parabola.model.plot(
    energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2
)
result_log_parabola.model.plot_error(
    energy_range=[1e-4, 1e2] * u.TeV, ax=ax, energy_power=2
)
ax.set_ylim(1e-13, 1e-11);
../_images/notebooks_sed_fitting_gammacat_fermi_31_0.png

Exercises

  • Fit a PowerLaw2 and ExponentialCutoffPowerLaw3FGL to the same data.
  • Fit a ExponentialCutoffPowerLaw model to Vela X (‘HESS J0835-455’) only and check if the best fit values correspond to the values given in the Gammacat catalog

What next?

This was an introduction to SED fitting in Gammapy.

  • If you would like to learn how to perform a full Poisson maximum likelihood spectral fit, please check out the spectrum pipe tutorial.
  • If you are interested in simulation of spectral data in the context of CTA, please check out the spectrum simulation cta notebook.
  • To learn more about other parts of Gammapy (e.g. Fermi-LAT and TeV data analysis), check out the other tutorial notebooks.
  • To see what’s available in Gammapy, browse the Gammapy docs or use the full-text search.
  • If you have any questions, ask on the mailing list .