This is a fixed-text formatted version of a Jupyter notebook

Fitting#

Prerequisites#

Proposed approach#

This is a hands-on tutorial to ~gammapy.modeling, showing how to do perform a Fit in gammapy. The emphasis here is on interfacing the Fit class and inspecting the errors. To see an analysis example of how datasets and models interact, see the model management notebook. As an example, in this notebook, we are going to work with HESS data of the Crab Nebula and show in particular how to : - perform a spectral analysis - use different fitting backends - access covariance matrix information and parameter errors - compute likelihood profile - compute confidence contours

See also: Models gallery tutorial and docs/modeling/index.rst.

The setup#

[1]:

import numpy as np
from astropy import units as u
import matplotlib.pyplot as plt
from matplotlib.ticker import StrMethodFormatter
import scipy.stats as st
from gammapy.modeling import Fit
from gammapy.datasets import Datasets, SpectrumDatasetOnOff
from gammapy.modeling.models import LogParabolaSpectralModel, SkyModel
from gammapy.visualization.utils import plot_contour_line
from itertools import combinations

Model and dataset#

First we define the source model, here we need only a spectral model for which we choose a log-parabola

[2]:

crab_spectrum = LogParabolaSpectralModel(
    amplitude=1e-11 / u.cm**2 / u.s / u.TeV,
    reference=1 * u.TeV,
    alpha=2.3,
    beta=0.2,
)

crab_spectrum.alpha.max = 3
crab_spectrum.alpha.min = 1
crab_model = SkyModel(spectral_model=crab_spectrum, name="crab")

The data and background are read from pre-computed ON/OFF datasets of HESS observations, for simplicity we stack them together. Then we set the model and fit range to the resulting dataset.

[3]:

datasets = []
for obs_id in [23523, 23526]:
    dataset = SpectrumDatasetOnOff.read(
        f"$GAMMAPY_DATA/joint-crab/spectra/hess/pha_obs{obs_id}.fits"
    )
    datasets.append(dataset)

dataset_hess = Datasets(datasets).stack_reduce(name="HESS")
datasets = Datasets(datasets=[dataset_hess])

# Set model and fit range
dataset_hess.models = crab_model
e_min = 0.66 * u.TeV
e_max = 30 * u.TeV
dataset_hess.mask_fit = dataset_hess.counts.geom.energy_mask(e_min, e_max)

Fitting options#

First let’s create a Fit instance:

[4]:

scipy_opts = {
    "method": "L-BFGS-B",
    "options": {"ftol": 1e-4, "gtol": 1e-05},
    "backend": "scipy",
}
fit_scipy = Fit(store_trace=True, optimize_opts=scipy_opts)

By default the fit is performed using MINUIT, you can select alternative optimizers and set their option using the optimize_opts argument of the Fit.run() method. In addition we have specified to store the trace of parameter values of the fit.

Note that, for now, covaraince matrix and errors are computed only for the fitting with MINUIT. However depending on the problem other optimizers can better perform, so sometimes it can be useful to run a pre-fit with alternative optimization methods.

For the “scipy” backend the available options are described in detail here:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
[5]:

%%time
result_scipy = fit_scipy.run(datasets)

CPU times: user 891 ms, sys: 6.08 ms, total: 897 ms
Wall time: 949 ms
For the “sherpa” backend you can choose the optimization algorithm between method = {“simplex”, “levmar”, “moncar”, “gridsearch”}.
Those methods are described and compared in detail on http://cxc.cfa.harvard.edu/sherpa/methods/index.html The available options of the optimization methods are described on the following page https://cxc.cfa.harvard.edu/sherpa/methods/opt_methods.html
[6]:

%%time
sherpa_opts = {"method": "simplex", "ftol": 1e-3, "maxfev": int(1e4)}
fit_sherpa = Fit(store_trace=True, backend="sherpa", optimize_opts=sherpa_opts)
results_simplex = fit_sherpa.run(datasets)

No covariance estimate - not supported by this backend.

CPU times: user 1.16 s, sys: 12.6 ms, total: 1.17 s
Wall time: 1.34 s

For the “minuit” backend see https://iminuit.readthedocs.io/en/latest/reference.html for a detailed description of the available options. If there is an entry ‘migrad_opts’, those options will be passed to iminuit.Minuit.migrad. Additionally you can set the fit tolerance using the tol option. The minimization will stop when the estimated distance to the minimum is less than 0.001*tol (by default tol=0.1). The strategy option change the speed and accuracy of the optimizer: 0 fast, 1 default, 2 slow but accurate. If you want more reliable error estimates, you should run the final fit with strategy 2.

[7]:

%%time
fit = Fit(store_trace=True)
minuit_opts = {"tol": 0.001, "strategy": 1}
fit.backend = "minuit"
fit.optimize_opts = minuit_opts
result_minuit = fit.run(datasets)

CPU times: user 334 ms, sys: 1.67 ms, total: 335 ms
Wall time: 364 ms

Fit quality assessment#

There are various ways to check the convergence and quality of a fit. Among them:

Refer to the automatically-generated results dictionary:

[8]:

print(result_scipy)

OptimizeResult

        backend    : scipy
        method     : L-BFGS-B
        success    : True
        message    : CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
        nfev       : 60
        total stat : 30.35

CovarianceResult

        backend    : minuit
        method     : hesse
        success    : True
        message    : Hesse terminated successfully.


[9]:

print(results_simplex)

OptimizeResult

        backend    : sherpa
        method     : simplex
        success    : True
        message    : Optimization terminated successfully
        nfev       : 135
        total stat : 30.35



[10]:

print(result_minuit)

OptimizeResult

        backend    : minuit
        method     : migrad
        success    : True
        message    : Optimization terminated successfully.
        nfev       : 37
        total stat : 30.35

CovarianceResult

        backend    : minuit
        method     : hesse
        success    : True
        message    : Hesse terminated successfully.

If the fit is performed with minuit you can print detailed informations to check the convergence

[11]:

print(fit.minuit)

┌─────────────────────────────────────────────────────────────────────────┐
│                                Migrad                                   │
├──────────────────────────────────┬──────────────────────────────────────┤
│ FCN = 30.35                      │              Nfcn = 37               │
│ EDM = 3.42e-08 (Goal: 2e-06)     │            time = 0.3 sec            │
├──────────────────────────────────┼──────────────────────────────────────┤
│          Valid Minimum           │        No Parameters at limit        │
├──────────────────────────────────┼──────────────────────────────────────┤
│ Below EDM threshold (goal x 10)  │           Below call limit           │
├───────────────┬──────────────────┼───────────┬─────────────┬────────────┤
│  Covariance   │     Hesse ok     │ Accurate  │  Pos. def.  │ Not forced │
└───────────────┴──────────────────┴───────────┴─────────────┴────────────┘
┌───┬───────────────────┬───────────┬───────────┬────────────┬────────────┬─────────┬─────────┬───────┐
│   │ Name              │   Value   │ Hesse Err │ Minos Err- │ Minos Err+ │ Limit-  │ Limit+  │ Fixed │
├───┼───────────────────┼───────────┼───────────┼────────────┼────────────┼─────────┼─────────┼───────┤
│ 0 │ par_000_amplitude │    3.8    │    0.4    │            │            │         │         │       │
│ 1 │ par_001_alpha     │   2.20    │   0.26    │            │            │    1    │    3    │       │
│ 2 │ par_002_beta      │    2.3    │    1.4    │            │            │         │         │       │
└───┴───────────────────┴───────────┴───────────┴────────────┴────────────┴─────────┴─────────┴───────┘
┌───────────────────┬───────────────────────────────────────────────────────┐
│                   │ par_000_amplitude     par_001_alpha      par_002_beta │
├───────────────────┼───────────────────────────────────────────────────────┤
│ par_000_amplitude │             0.126            0.0455            -0.117 │
│     par_001_alpha │            0.0455            0.0689            -0.331 │
│      par_002_beta │            -0.117            -0.331              1.95 │
└───────────────────┴───────────────────────────────────────────────────────┘

Check the trace of the fit e.g. in case the fit did not converge properly

[12]:

result_minuit.trace

[12]:
Table length=37
total_statcrab.spectral.amplitudecrab.spectral.alphacrab.spectral.beta
float64float64float64float64
30.3495305503252553.8122425674284106e-112.19574690918057550.22648273578364578
30.3497246009786753.815794007969182e-112.19574690918057550.22648273578364578
30.349711761511393.808691126887639e-112.19574690918057550.22648273578364578
30.3495393265193383.812951390605948e-112.19574690918057550.22648273578364578
30.349536722746763.811533744250873e-112.19574690918057550.22648273578364578
30.35051042287283.8122425674284106e-112.1984267051995310.22648273578364578
30.350545513858923.8122425674284106e-112.1930656506336420.22648273578364578
30.3495390066514553.8122425674284106e-112.1960149549266820.22648273578364578
30.3495420423346223.8122425674284106e-112.19547884880918030.22648273578364578
30.3502964092421553.8122425674284106e-112.19574690918057550.2278906654195459
30.350334084456513.8122425674284106e-112.19574690918057550.22507480614774567
30.3495367558950773.8122425674284106e-112.19574690918057550.2266235287472358
30.3495400385776543.8122425674284106e-112.19574690918057550.22634194282005576
30.3495306328424163.8121808354793116e-112.19576730492930850.2264974606416853
30.349530467387433.812216974144315e-112.19575536500990860.22648884052325902
............
30.3495379824220923.812925797449946e-112.19575536500990860.22648884052325902
30.349537901135253.811508150838685e-112.19575536500990860.22648884052325902
30.349538145414363.812216974144315e-112.1959874018794360.22648884052325902
30.3495377371049673.812216974144315e-112.1955233171802020.22648884052325902
30.3495378044984363.812216974144315e-112.19575536500990860.22662625014703108
30.3495380777865263.812216974144315e-112.19575536500990860.22635143089948695
30.349530774655723.8123587388054416e-112.19575536500990860.22648884052325902
30.3495307580703233.8120752094831896e-112.19575536500990860.22648884052325902
30.349530807471043.812216974144315e-112.19580177326104440.22648884052325902
30.3495307252135483.812216974144315e-112.19570895632036620.22648884052325902
30.34953073944583.812216974144315e-112.19575536500990860.22651632244801345
30.349530793229383.812216974144315e-112.19575536500990860.2264613585985046
30.3495358149617943.812925797449946e-112.1959874018794360.22648884052325902
30.349537158919583.812925797449946e-112.19575536500990860.22662625014703108
30.3495593669196073.812216974144315e-112.1959874018794360.22662625014703108

Check that the fitted values and errors for all parameters are reasonable, and no fitted parameter value is “too close” - or even outside - its allowed min-max range

[13]:

result_minuit.parameters.to_table()

[13]:
Table length=4
typenamevalueuniterrorminmaxfrozenis_normlink
str8str9float64str14float64float64float64boolboolstr1
spectralamplitude3.8122e-11cm-2 s-1 TeV-13.546e-12nannanFalseTrue
spectralreference1.0000e+00TeV0.000e+00nannanTrueFalse
spectralalpha2.1958e+002.626e-011.000e+003.000e+00FalseFalse
spectralbeta2.2649e-011.397e-01nannanFalseFalse

Plot fit statistic profiles for all fitted parameters, using gammapy.modeling.Fit.stat_profile(). For a good fit and error estimate each profile should be parabolic. The specification for each fit statistic profile can be changed on the gammapy.modeling.Parameter object, which has .scan_min, .scan_max, .scan_n_values and .scan_n_sigma attributes.

[14]:

total_stat = result_minuit.total_stat

fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(14, 4))

for ax, par in zip(axes, crab_model.parameters.free_parameters):
    par.scan_n_values = 17

    profile = fit.stat_profile(datasets=datasets, parameter=par)
    ax.plot(profile[f"{par.name}_scan"], profile["stat_scan"] - total_stat)
    ax.set_xlabel(f"{par.unit}")
    ax.set_ylabel("Delta TS")
    ax.set_title(f"{par.name}: {par.value:.1e} +- {par.error:.1e}")
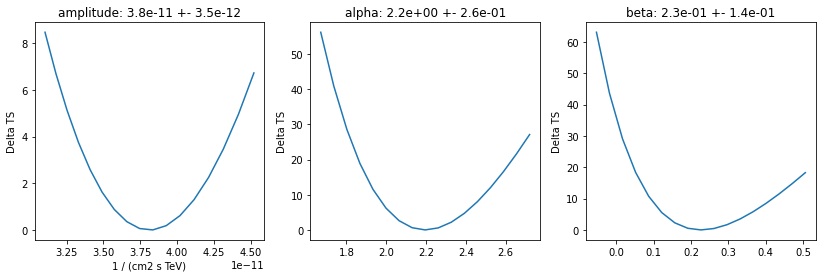
../../_images/tutorials_api_fitting_26_0.png

Inspect model residuals. Those can always be accessed using ~Dataset.residuals(), that will return an array in case a the fitted Dataset is a SpectrumDataset and a full cube in case of a MapDataset. For more details, we refer here to the dedicated fitting tutorials: analysis_3d.ipynb (for MapDataset fitting) and spectrum_analysis.ipynb (for SpectrumDataset fitting).

Covariance and parameters errors#

After the fit the covariance matrix is attached to the model. You can get the error on a specific parameter by accessing the .error attribute:

[15]:

crab_model.spectral_model.alpha.error

[15]:

0.2625818137415194

And you can plot the total parameter correlation as well:

[16]:

crab_model.covariance.plot_correlation()

[16]:

<AxesSubplot:>
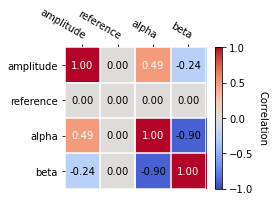
../../_images/tutorials_api_fitting_31_1.png

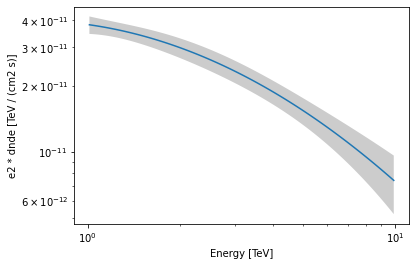
As an example, this step is needed to produce a butterfly plot showing the envelope of the model taking into account parameter uncertainties.

[17]:

energy_bounds = [1, 10] * u.TeV
crab_spectrum.plot(energy_bounds=energy_bounds, energy_power=2)
ax = crab_spectrum.plot_error(energy_bounds=energy_bounds, energy_power=2)
../../_images/tutorials_api_fitting_33_0.png

Confidence contours#

In most studies, one wishes to estimate parameters distribution using observed sample data. A 1-dimensional confidence interval gives an estimated range of values which is likely to include an unknown parameter. A confidence contour is a 2-dimensional generalization of a confidence interval, often represented as an ellipsoid around the best-fit value.

Gammapy offers two ways of computing confidence contours, in the dedicated methods Fit.minos_contour() and Fit.stat_profile(). In the following sections we will describe them.

An important point to keep in mind is: what does a :math:`Nsigma` confidence contour really mean? The answer is it represents the points of the parameter space for which the model likelihood is \(N\sigma\) above the minimum. But one always has to keep in mind that 1 standard deviation in two dimensions has a smaller coverage probability than 68%, and similarly for all other levels. In particular, in 2-dimensions the probability enclosed by the \(N\sigma\) confidence contour is \(P(N)=1-e^{-N^2/2}\).

Computing contours using Fit.stat_contour()#

After the fit, MINUIT offers the possibility to compute the confidence confours. gammapy provides an interface to this functionality through the Fit object using the .stat_contour method. Here we defined a function to automate the contour production for the different parameterer and confidence levels (expressed in term of sigma):

[18]:

def make_contours(fit, datasets, result, npoints, sigmas):
    cts_sigma = []
    for sigma in sigmas:
        contours = dict()
        for par_1, par_2 in combinations(["alpha", "beta", "amplitude"], r=2):
            contour = fit.stat_contour(
                datasets=datasets,
                x=datasets.parameters[par_1],
                y=datasets.parameters[par_2],
                numpoints=npoints,
                sigma=sigma,
            )
            contours[f"contour_{par_1}_{par_2}"] = {
                par_1: contour[par_1].tolist(),
                par_2: contour[par_2].tolist(),
            }
        cts_sigma.append(contours)
    return cts_sigma

Now we can compute few contours.

[19]:

%%time
sigmas = [1, 2]
cts_sigma = make_contours(
    fit=fit,
    datasets=datasets,
    result=result_minuit,
    npoints=10,
    sigmas=sigmas,
)

CPU times: user 29.3 s, sys: 88.5 ms, total: 29.3 s
Wall time: 31.5 s

Then we prepare some aliases and annotations in order to make the plotting nicer.

[20]:

pars = {
    "phi": r"$\phi_0 \,/\,(10^{-11}\,{\rm TeV}^{-1} \, {\rm cm}^{-2} {\rm s}^{-1})$",
    "alpha": r"$\alpha$",
    "beta": r"$\beta$",
}

panels = [
    {
        "x": "alpha",
        "y": "phi",
        "cx": (lambda ct: ct["contour_alpha_amplitude"]["alpha"]),
        "cy": (
            lambda ct: np.array(1e11)
            * ct["contour_alpha_amplitude"]["amplitude"]
        ),
    },
    {
        "x": "beta",
        "y": "phi",
        "cx": (lambda ct: ct["contour_beta_amplitude"]["beta"]),
        "cy": (
            lambda ct: np.array(1e11)
            * ct["contour_beta_amplitude"]["amplitude"]
        ),
    },
    {
        "x": "alpha",
        "y": "beta",
        "cx": (lambda ct: ct["contour_alpha_beta"]["alpha"]),
        "cy": (lambda ct: ct["contour_alpha_beta"]["beta"]),
    },
]

Finally we produce the confidence contours figures.

[21]:

fig, axes = plt.subplots(1, 3, figsize=(16, 5))
colors = ["m", "b", "c"]
for p, ax in zip(panels, axes):
    xlabel = pars[p["x"]]
    ylabel = pars[p["y"]]
    for ks in range(len(cts_sigma)):
        plot_contour_line(
            ax,
            p["cx"](cts_sigma[ks]),
            p["cy"](cts_sigma[ks]),
            lw=2.5,
            color=colors[ks],
            label=f"{sigmas[ks]}" + r"$\sigma$",
        )
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
plt.legend()
plt.tight_layout()
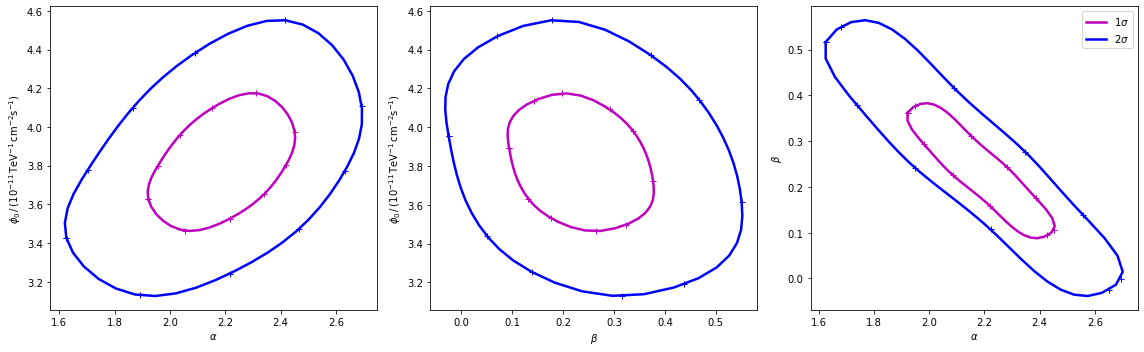
../../_images/tutorials_api_fitting_44_0.png

Computing contours using Fit.stat_surface()#

This alternative method for the computation of confidence contours, although more time consuming than Fit.minos_contour(), is expected to be more stable. It consists of a generalization of Fit.stat_profile() to a 2-dimensional parameter space. The algorithm is very simple: - First, passing two arrays of parameters values, a 2-dimensional discrete parameter space is defined; - For each node of the parameter space, the two parameters of interest are frozen. This way, a likelihood value (\(-2\mathrm{ln}\,\mathcal{L}\), actually) is computed, by either freezing (default) or fitting all nuisance parameters; - Finally, a 2-dimensional surface of \(-2\mathrm{ln}(\mathcal{L})\) values is returned. Using that surface, one can easily compute a surface of \(TS = -2\Delta\mathrm{ln}(\mathcal{L})\) and compute confidence contours.

Let’s see it step by step.

First of all, we can notice that this method is “backend-agnostic”, meaning that it can be run with MINUIT, sherpa or scipy as fitting tools. Here we will stick with MINUIT, which is the default choice:

[ ]:

As an example, we can compute the confidence contour for the alpha and beta parameters of the dataset_hess. Here we define the parameter space:

[22]:

result = result_minuit
par_alpha = datasets.parameters["alpha"]
par_beta = datasets.parameters["beta"]

par_alpha.scan_values = np.linspace(1.55, 2.7, 20)
par_beta.scan_values = np.linspace(-0.05, 0.55, 20)

Then we run the algorithm, by choosing reoptimize=False for the sake of time saving. In real life applications, we strongly recommend to use reoptimize=True, so that all free nuisance parameters will be fit at each grid node. This is the correct way, statistically speaking, of computing confidence contours, but is expected to be time consuming.

[23]:

fit = Fit(backend="minuit", optimize_opts={"print_level": 0})
stat_surface = fit.stat_surface(
    datasets=datasets,
    x=par_alpha,
    y=par_beta,
    reoptimize=False,
)

In order to easily inspect the results, we can convert the \(-2\mathrm{ln}(\mathcal{L})\) surface to a surface of statistical significance (in units of Gaussian standard deviations from the surface minimum):

[24]:

# Compute TS
TS = stat_surface["stat_scan"] - result.total_stat

[25]:

# Compute the corresponding statistical significance surface
stat_surface = np.sqrt(TS.T)

Notice that, as explained before, \(1\sigma\) contour obtained this way will not contain 68% of the probability, but rather

[26]:

# Compute the corresponding statistical significance surface
# p_value = 1 - st.chi2(df=1).cdf(TS)
# gaussian_sigmas = st.norm.isf(p_value / 2).T

Finally, we can plot the surface values together with contours:

[27]:

fig, ax = plt.subplots(figsize=(8, 6))
x_values = par_alpha.scan_values
y_values = par_beta.scan_values

# plot surface
im = ax.pcolormesh(x_values, y_values, stat_surface, shading="auto")
fig.colorbar(im, label="sqrt(TS)")
ax.set_xlabel(f"{par_alpha.name}")
ax.set_ylabel(f"{par_beta.name}")

# We choose to plot 1 and 2 sigma confidence contours
levels = [1, 2]
contours = ax.contour(
    x_values, y_values, stat_surface, levels=levels, colors="white"
)
ax.clabel(contours, fmt="%.0f$\,\sigma$", inline=3, fontsize=15);
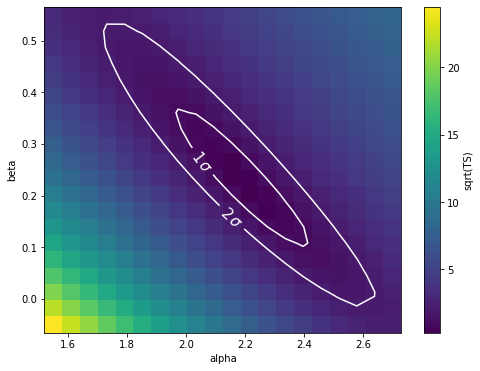
../../_images/tutorials_api_fitting_59_0.png

Note that, if computed with reoptimize=True, this plot would be completely consistent with the third panel of the plot produced with Fit.stat_contour (try!).

Finally, it is always remember that confidence contours are approximations. In particular, when the parameter range boundaries are close to the contours lines, it is expected that the statistical meaning of the contours is not well defined. That’s why we advise to always choose a parameter space that com contain the contours you’re interested in.

[ ]: