This is a fixed-text formatted version of a Jupyter notebook

Try online
You can contribute with your own notebooks in this GitHub repository.
Source files: analysis_3d.ipynb | analysis_3d.py

3D analysis¶

This tutorial shows how to run a stacked 3D map-based analysis using three example observations of the Galactic center region with CTA.

Setup¶

[1]:

%matplotlib inline
import matplotlib.pyplot as plt

[2]:

from pathlib import Path
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from gammapy.data import DataStore
from gammapy.irf import EnergyDispersion, make_mean_psf, make_mean_edisp
from gammapy.maps import WcsGeom, MapAxis, Map, WcsNDMap
from gammapy.cube import MapMaker, PSFKernel, MapDataset
from gammapy.modeling.models import (
    SkyModel,
    SkyDiffuseCube,
    BackgroundModel,
    PowerLawSpectralModel,
    ExpCutoffPowerLawSpectralModel,
    PointSpatialModel,
)
from gammapy.spectrum import FluxPointsEstimator
from gammapy.modeling import Fit

Prepare modeling input data¶

Prepare input maps¶

We first use the DataStore object to access the CTA observations and retrieve a list of observations by passing the observations IDs to the .get_observations() method:

[3]:

# Define which data to use and print some information
data_store = DataStore.from_dir("$GAMMAPY_DATA/cta-1dc/index/gps/")
data_store.info()
print(
    "Observation time (hours): ", data_store.obs_table["ONTIME"].sum() / 3600
)
print("Observation table: ", data_store.obs_table.colnames)
print("HDU table: ", data_store.hdu_table.colnames)

Data store:
HDU index table:
BASE_DIR: /Users/adonath/data/gammapy-data/cta-1dc/index/gps
Rows: 24
OBS_ID: 110380 -- 111630
HDU_TYPE: ['aeff', 'bkg', 'edisp', 'events', 'gti', 'psf']
HDU_CLASS: ['aeff_2d', 'bkg_3d', 'edisp_2d', 'events', 'gti', 'psf_3gauss']


Observation table:
Observatory name: 'N/A'
Number of observations: 4

Observation time (hours):  2.0
Observation table:  ['OBS_ID', 'RA_PNT', 'DEC_PNT', 'GLON_PNT', 'GLAT_PNT', 'ZEN_PNT', 'ALT_PNT', 'AZ_PNT', 'ONTIME', 'LIVETIME', 'DEADC', 'TSTART', 'TSTOP', 'DATE-OBS', 'TIME-OBS', 'DATE-END', 'TIME-END', 'N_TELS', 'OBJECT', 'CALDB', 'IRF', 'EVENTS_FILENAME', 'EVENT_COUNT']
HDU table:  ['OBS_ID', 'HDU_TYPE', 'HDU_CLASS', 'FILE_DIR', 'FILE_NAME', 'HDU_NAME']

[4]:

# Select some observations from these dataset by hand
obs_ids = [110380, 111140, 111159]
observations = data_store.get_observations(obs_ids)

Now we define a reference geometry for our analysis, We choose a WCS based gemoetry with a binsize of 0.02 deg and also define an energy axis:

[5]:

energy_axis = MapAxis.from_edges(
    np.logspace(-1.0, 1.0, 10), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
    skydir=(0, 0),
    binsz=0.02,
    width=(10, 8),
    coordsys="GAL",
    proj="CAR",
    axes=[energy_axis],
)

The MapMaker object is initialized with this reference geometry and a field of view cut of 4 deg:

[6]:

%%time
maker = MapMaker(geom, offset_max=4.0 * u.deg)
maps = maker.run(observations)

WARNING: Tried to get polar motions for times after IERS data is valid. Defaulting to polar motion from the 50-yr mean for those. This may affect precision at the 10s of arcsec level [astropy.coordinates.builtin_frames.utils]
/Users/adonath/github/adonath/gammapy/gammapy/utils/interpolation.py:159: Warning: Interpolated values reached float32 precision limit
  "Interpolated values reached float32 precision limit", Warning

CPU times: user 13.3 s, sys: 2.41 s, total: 15.7 s
Wall time: 15.7 s

The maps are prepared by calling the .run() method and passing the observations. The .run() method returns a Python dict containing a counts, background and exposure map:

[7]:

print(maps)

{'counts': WcsNDMap

        geom  : WcsGeom
        axes  : ['lon', 'lat', 'energy']
        shape : (500, 400, 9)
        ndim  : 3
        unit  :
        dtype : float32
, 'exposure': WcsNDMap

        geom  : WcsGeom
        axes  : ['lon', 'lat', 'energy']
        shape : (500, 400, 9)
        ndim  : 3
        unit  : m2 s
        dtype : float32
, 'background': WcsNDMap

        geom  : WcsGeom
        axes  : ['lon', 'lat', 'energy']
        shape : (500, 400, 9)
        ndim  : 3
        unit  :
        dtype : float64
}

This is what the summed counts image looks like:

[8]:

counts = maps["counts"].sum_over_axes()
counts.smooth(width=0.1 * u.deg).plot(stretch="sqrt", add_cbar=True, vmax=6);

../_images/notebooks_analysis_3d_15_0.png

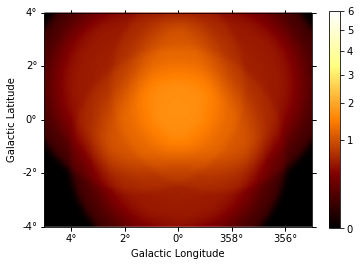
This is the background image:

[9]:

background = maps["background"].sum_over_axes()
background.smooth(width=0.1 * u.deg).plot(
    stretch="sqrt", add_cbar=True, vmax=6
);

../_images/notebooks_analysis_3d_17_0.png

And this one the exposure image:

[10]:

exposure = maps["exposure"].sum_over_axes()
exposure.smooth(width=0.1 * u.deg).plot(stretch="sqrt", add_cbar=True);

../_images/notebooks_analysis_3d_19_0.png

We can also compute an excess image just with a few lines of code:

[11]:

excess = counts - background
excess.smooth(5).plot(stretch="sqrt", add_cbar=True);

../_images/notebooks_analysis_3d_21_0.png

For a more realistic excess plot we can also take into account the diffuse galactic emission. For this tutorial we will load a Fermi diffuse model map that represents a small cutout for the Galactic center region:

[12]:

diffuse_gal = Map.read("$GAMMAPY_DATA/fermi-3fhl-gc/gll_iem_v06_gc.fits.gz")

[13]:

print("Diffuse image: ", diffuse_gal.geom)
print("counts: ", maps["counts"].geom)

Diffuse image:  WcsGeom

        axes       : ['lon', 'lat', 'energy']
        shape      : (120, 64, 30)
        ndim       : 3
        coordsys   : GAL
        projection : CAR
        center     : 0.0 deg, -0.1 deg
        width      : 15.0 deg x 8.0 deg

counts:  WcsGeom

        axes       : ['lon', 'lat', 'energy']
        shape      : (500, 400, 9)
        ndim       : 3
        coordsys   : GAL
        projection : CAR
        center     : 0.0 deg, 0.0 deg
        width      : 10.0 deg x 8.0 deg

We see that the geometry of the images is completely different, so we need to apply our geometric configuration to the diffuse emission file:

[14]:

coord = maps["counts"].geom.get_coord()

data = diffuse_gal.interp_by_coord(
    {"skycoord": coord.skycoord, "energy": coord["energy"]}, interp=3
)
diffuse_galactic = WcsNDMap(maps["counts"].geom, data)
print("Before: \n", diffuse_gal.geom)
print("Now (same as maps): \n", diffuse_galactic.geom)

Before:
 WcsGeom

        axes       : ['lon', 'lat', 'energy']
        shape      : (120, 64, 30)
        ndim       : 3
        coordsys   : GAL
        projection : CAR
        center     : 0.0 deg, -0.1 deg
        width      : 15.0 deg x 8.0 deg

Now (same as maps):
 WcsGeom

        axes       : ['lon', 'lat', 'energy']
        shape      : (500, 400, 9)
        ndim       : 3
        coordsys   : GAL
        projection : CAR
        center     : 0.0 deg, 0.0 deg
        width      : 10.0 deg x 8.0 deg

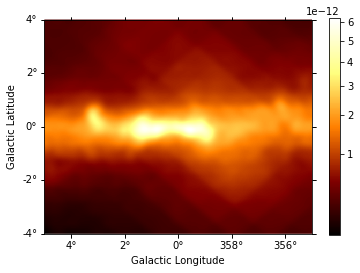
[15]:

# diffuse_galactic.slice_by_idx({"energy": 0}).plot(add_cbar=True); # this can be used to check image at different energy bins
diffuse = diffuse_galactic.sum_over_axes()
diffuse.smooth(5).plot(stretch="sqrt", add_cbar=True)
print(diffuse)

WcsNDMap

        geom  : WcsGeom
        axes  : ['lon', 'lat']
        shape : (500, 400)
        ndim  : 2
        unit  :
        dtype : float32

../_images/notebooks_analysis_3d_27_1.png

We now multiply the exposure for this diffuse emission to subtract the result from the counts along with the background.

[16]:

combination = diffuse * exposure
combination.unit = ""
combination.smooth(5).plot(stretch="sqrt", add_cbar=True);

../_images/notebooks_analysis_3d_29_0.png

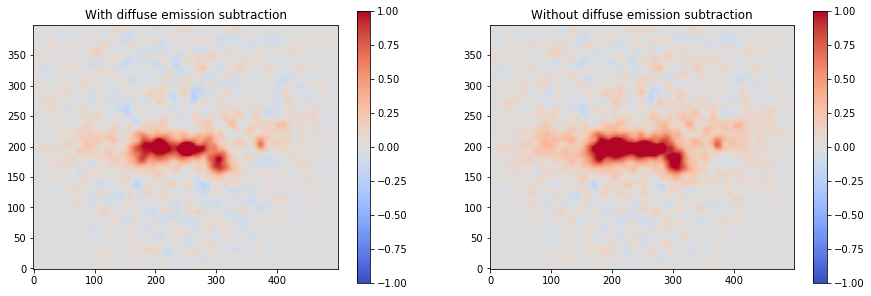
We can plot then the excess image subtracting now the effect of the diffuse galactic emission.

[17]:

excess2 = counts - background - combination

fig, axs = plt.subplots(1, 2, figsize=(15, 5))

axs[0].set_title("With diffuse emission subtraction")
axs[1].set_title("Without diffuse emission subtraction")
excess2.smooth(5).plot(
    cmap="coolwarm", vmin=-1, vmax=1, add_cbar=True, ax=axs[0]
)
excess.smooth(5).plot(
    cmap="coolwarm", vmin=-1, vmax=1, add_cbar=True, ax=axs[1]
);

../_images/notebooks_analysis_3d_31_0.png

Prepare IRFs¶

To estimate the mean PSF across all observations at a given source position src_pos, we use make_mean_psf():

[18]:

# mean PSF
src_pos = SkyCoord(0, 0, unit="deg", frame="galactic")
table_psf = make_mean_psf(observations, src_pos)

# PSF kernel used for the model convolution
psf_kernel = PSFKernel.from_table_psf(table_psf, geom, max_radius="0.3 deg")

To estimate the mean energy dispersion across all observations at a given source position src_pos, we use make_mean_edisp():

[19]:

# define energy grid
energy = energy_axis.edges

# mean edisp
edisp = make_mean_edisp(
    observations, position=src_pos, e_true=energy, e_reco=energy
)

/Users/adonath/github/adonath/gammapy/gammapy/utils/interpolation.py:159: Warning: Interpolated values reached float32 precision limit
  "Interpolated values reached float32 precision limit", Warning

Save maps and IRFs to disk¶

It is common to run the preparation step independent of the likelihood fit, because often the preparation of maps, PSF and energy dispersion is slow if you have a lot of data. We first create a folder:

[20]:

path = Path("analysis_3d")
path.mkdir(exist_ok=True)

And then write the maps and IRFs to disk by calling the dedicated .write() methods:

[21]:

# write maps
maps["counts"].write(str(path / "counts.fits"), overwrite=True)
maps["background"].write(str(path / "background.fits"), overwrite=True)
maps["exposure"].write(str(path / "exposure.fits"), overwrite=True)

# write IRFs
psf_kernel.write(str(path / "psf.fits"), overwrite=True)
edisp.write(str(path / "edisp.fits"), overwrite=True)

Likelihood fit¶

Reading maps and IRFs¶

As first step we read in the maps and IRFs that we have saved to disk again:

[22]:

# read maps
maps = {
    "counts": Map.read(str(path / "counts.fits")),
    "background": Map.read(str(path / "background.fits")),
    "exposure": Map.read(str(path / "exposure.fits")),
}

# read IRFs
psf_kernel = PSFKernel.read(str(path / "psf.fits"))
edisp = EnergyDispersion.read(str(path / "edisp.fits"))

Fit mask¶

To select a certain energy range for the fit we can create a fit mask:

[23]:

coords = maps["counts"].geom.get_coord()
mask = coords["energy"] > 0.3 * u.TeV

Model fit¶

No we are ready for the actual likelihood fit. We first define the model as a combination of a point source with a powerlaw:

[24]:

spatial_model = PointSpatialModel(
    lon_0="0.01 deg", lat_0="0.01 deg", frame="galactic"
)
spectral_model = PowerLawSpectralModel(
    index=2.2, amplitude="3e-12 cm-2 s-1 TeV-1", reference="1 TeV"
)
model = SkyModel(spatial_model=spatial_model, spectral_model=spectral_model)

Often, it is useful to fit the normalization (and also the tilt) of the background. To do so, we have to define the background as a model. In this example, we will keep the tilt fixed and the norm free.

[25]:

background_model = BackgroundModel(maps["background"], norm=1.1, tilt=0.0)
background_model.parameters["norm"].frozen = False
background_model.parameters["tilt"].frozen = True

Now we set up the MapDataset object by passing the prepared maps, IRFs as well as the model:

[26]:

dataset = MapDataset(
    model=model,
    counts=maps["counts"],
    exposure=maps["exposure"],
    background_model=background_model,
    mask_fit=mask,
    psf=psf_kernel,
    edisp=edisp,
)

No we run the model fit:

[27]:

%%time
fit = Fit(dataset)
result = fit.run(optimize_opts={"print_level": 1})

------------------------------------------------------------------
| FCN = 3.182E+05               |     Ncalls=153 (153 total)     |
| EDM = 2.8E-05 (Goal: 1E-05)   |            up = 1.0            |
------------------------------------------------------------------
|  Valid Min.   | Valid Param.  | Above EDM | Reached call limit |
------------------------------------------------------------------
|     True      |     True      |   False   |       False        |
------------------------------------------------------------------
| Hesse failed  |   Has cov.    | Accurate  | Pos. def. | Forced |
------------------------------------------------------------------
|     False     |     True      |   True    |   True    | False  |
------------------------------------------------------------------
CPU times: user 3.89 s, sys: 935 ms, total: 4.83 s
Wall time: 4.83 s

[28]:

result.parameters.to_table()

[28]:

Table length=8

name	value	error	unit	min	max	frozen
str9	float64	float64	str14	float64	float64	bool
lon_0	-4.820e-02	2.192e-03	deg	nan	nan	False
lat_0	-4.880e-02	2.166e-03	deg	-9.000e+01	9.000e+01	False
index	2.385e+00	6.003e-02		nan	nan	False
amplitude	2.735e-12	1.501e-13	cm-2 s-1 TeV-1	nan	nan	False
reference	1.000e+00	0.000e+00	TeV	nan	nan	True
norm	1.236e+00	5.991e-03		0.000e+00	nan	False
tilt	0.000e+00	0.000e+00		nan	nan	True
reference	1.000e+00	0.000e+00	TeV	nan	nan	True

Check model fit¶

We check the model fit by computing a residual image. For this we first get the number of predicted counts:

[29]:

npred = dataset.npred()

And compute a residual image:

[30]:

residual = maps["counts"] - npred

[31]:

residual.sum_over_axes().smooth(width=0.05 * u.deg).plot(
    cmap="coolwarm", vmin=-1, vmax=1, add_cbar=True
);

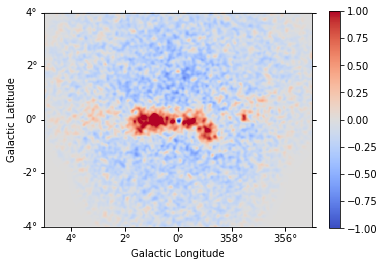
../_images/notebooks_analysis_3d_57_0.png

We can also plot the best fit spectrum. For that need to extract the covariance of the spectral parameters.

[32]:

spec = model.spectral_model

# set covariance on the spectral model
covariance = result.parameters.covariance
spec.parameters.covariance = covariance[2:5, 2:5]

energy_range = [0.3, 10] * u.TeV
spec.plot(energy_range=energy_range, energy_power=2)
spec.plot_error(energy_range=energy_range, energy_power=2)

[32]:

<matplotlib.axes._subplots.AxesSubplot at 0x124116358>

../_images/notebooks_analysis_3d_59_1.png

Apparently our model should be improved by adding a component for diffuse Galactic emission and at least one second point source.

Add Galactic diffuse emission to model¶

We use both models at the same time, our diffuse model (the same from the Fermi file used before) and our model for the central source. This time, in order to make it more realistic, we will consider an exponential cut off power law spectral model for the source. We will fit again the normalization and tilt of the background.

[33]:

diffuse_model = SkyDiffuseCube.read(
    "$GAMMAPY_DATA/fermi-3fhl-gc/gll_iem_v06_gc.fits.gz"
)

[34]:

spatial_model = PointSpatialModel(
    lon_0="-0.05 deg", lat_0="-0.05 deg", frame="galactic"
)
spectral_model = ExpCutoffPowerLawSpectralModel(
    index=2,
    amplitude=3e-12 * u.Unit("cm-2 s-1 TeV-1"),
    reference=1.0 * u.TeV,
    lambda_=0.1 / u.TeV,
)

model_ecpl = SkyModel(
    spatial_model=spatial_model,
    spectral_model=spectral_model,
    name="gc-source",
)

[35]:

dataset_combined = MapDataset(
    model=model_ecpl + diffuse_model,
    counts=maps["counts"],
    exposure=maps["exposure"],
    background_model=background_model,
    psf=psf_kernel,
    edisp=edisp,
)

[36]:

%%time
fit_combined = Fit(dataset_combined)
result_combined = fit_combined.run()

CPU times: user 43.6 s, sys: 4.61 s, total: 48.2 s
Wall time: 48.2 s

As we can see we have now two components in our model, and we can access them separately.

[37]:

# Checking normalization value (the closer to 1 the better)
print(model_ecpl, "\n")
print(background_model, "\n")
print(diffuse_model, "\n")

SkyModel

Parameters:

           name     value    error      unit         min        max    frozen
        --------- ---------- ----- -------------- ---------- --------- ------
            lon_0 -4.810e-02   nan            deg        nan       nan  False
            lat_0 -5.245e-02   nan            deg -9.000e+01 9.000e+01  False
            index  2.213e+00   nan                       nan       nan  False
        amplitude  2.786e-12   nan cm-2 s-1 TeV-1        nan       nan  False
        reference  1.000e+00   nan            TeV        nan       nan   True
          lambda_  4.429e-02   nan          TeV-1        nan       nan  False

BackgroundModel

Parameters:

           name     value   error unit    min    max frozen
        --------- --------- ----- ---- --------- --- ------
             norm 1.052e+00   nan      0.000e+00 nan  False
             tilt 0.000e+00   nan            nan nan   True
        reference 1.000e+00   nan  TeV       nan nan   True

SkyDiffuseCube

Parameters:

           name     value   error unit min max frozen
        --------- --------- ----- ---- --- --- ------
             norm 9.060e-01   nan      nan nan  False
             tilt 0.000e+00   nan      nan nan   True
        reference 1.000e+00   nan  TeV nan nan   True

You can see that the normalization of the background has vastly improved

We can now plot the residual image considering this improved model.

[38]:

residual2 = maps["counts"] - dataset_combined.npred()

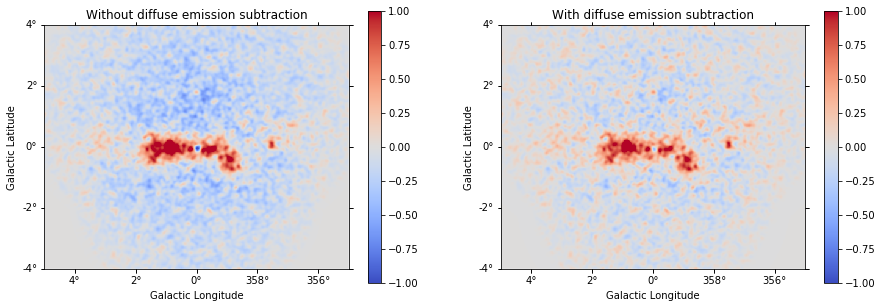
Just as a comparison, we can plot our previous residual map (left) and the new one (right) with the same scale:

[39]:

plt.figure(figsize=(15, 5))
ax_1 = plt.subplot(121, projection=residual.geom.wcs)
ax_2 = plt.subplot(122, projection=residual.geom.wcs)

ax_1.set_title("Without diffuse emission subtraction")
ax_2.set_title("With diffuse emission subtraction")

residual.sum_over_axes().smooth(width=0.05 * u.deg).plot(
    cmap="coolwarm", vmin=-1, vmax=1, add_cbar=True, ax=ax_1
)
residual2.sum_over_axes().smooth(width=0.05 * u.deg).plot(
    cmap="coolwarm", vmin=-1, vmax=1, add_cbar=True, ax=ax_2
);

../_images/notebooks_analysis_3d_73_0.png

Computing Flux Points¶

Finally we compute flux points for the galactic center source. For this we first define an energy binning:

[40]:

e_edges = [0.3, 1, 3, 10] * u.TeV
fpe = FluxPointsEstimator(
    datasets=[dataset_combined], e_edges=e_edges, source="gc-source"
)

[41]:

%%time
flux_points = fpe.run()

CPU times: user 19.4 s, sys: 2 s, total: 21.4 s
Wall time: 21.4 s

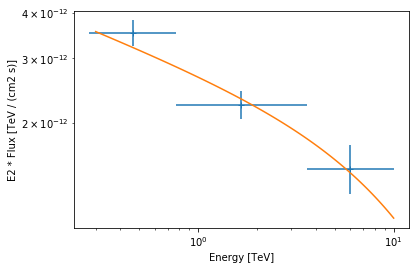
Now let’s plot the best fit model and flux points:

[42]:

flux_points.table["is_ul"] = flux_points.table["ts"] < 4
ax = flux_points.plot(energy_power=2)
model_ecpl.spectral_model.plot(
    ax=ax, energy_range=energy_range, energy_power=2
);

../_images/notebooks_analysis_3d_78_0.png

Summary¶

Note that this notebook aims to show you the procedure of a 3D analysis using just a few observations and a cutted Fermi model. Results get much better for a more complete analysis considering the GPS dataset from the CTA First Data Challenge (DC-1) and also the CTA model for the Galactic diffuse emission, as shown in the next image:

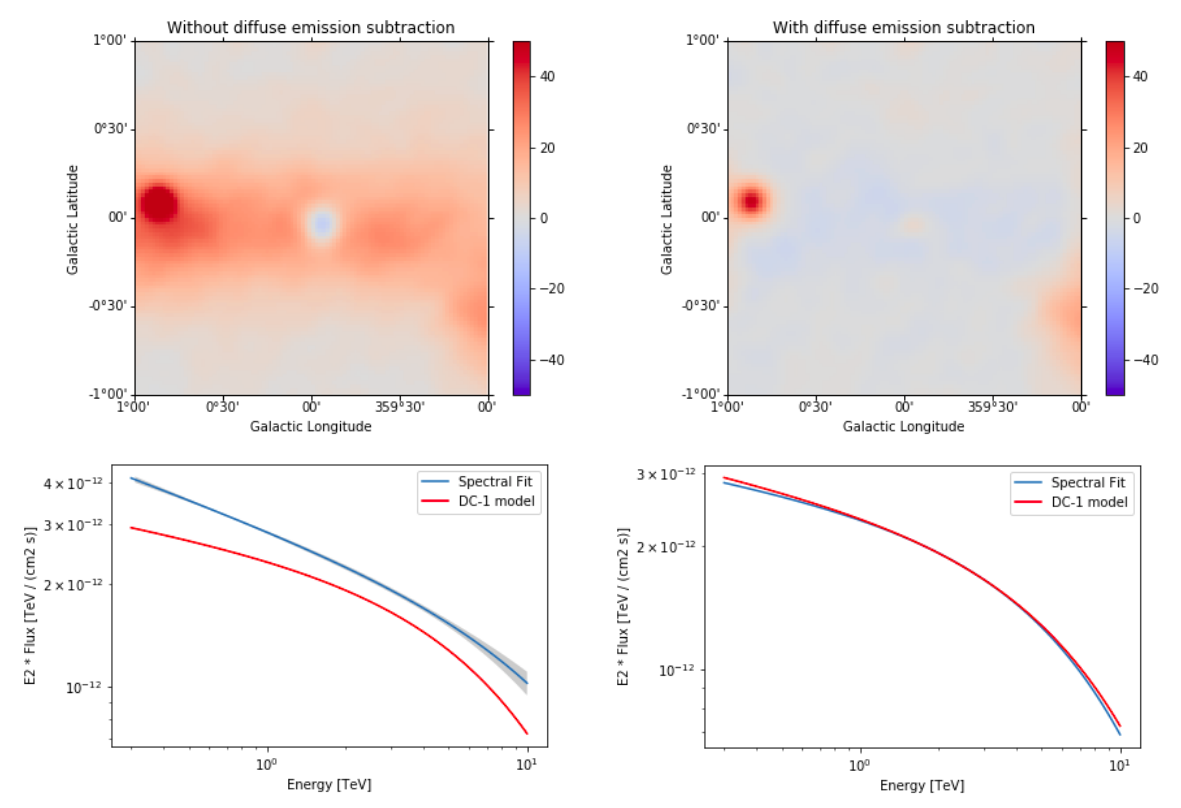
The complete tutorial notebook of this analysis is available to be downloaded in GAMMAPY-EXTRA repository at https://github.com/gammapy/gammapy-extra/blob/master/analyses/cta_1dc_gc_3d.ipynb).

Exercises¶

Analyse the second source in the field of view: G0.9+0.1 and add it to the combined model.