Energy Dispersion¶
as a function of of true energy and offset angle (EDISP_2D)¶
The EnergyDispersion2D class represents the probability density of the energy migration
\(\mu=\frac{E}{E_{\rm true}}\) as a function of true energy and offset angle from the field of view center
(\(E_{\rm disp}(E_{\rm true}, \mu|p_{\rm true})\) in IRF Theory).
Its format specifications are available in EDISP_2D
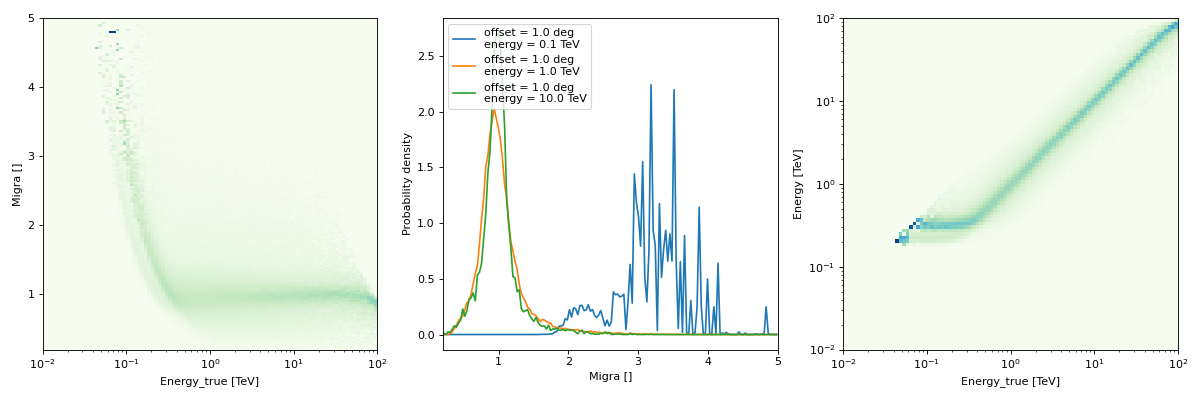
This is the format in which IACT DL3 energy dispersions are usually provided, as an example:
"""Plot an energy dispersion from the HESS DL3 data release 1."""
import matplotlib.pyplot as plt
from gammapy.irf import EnergyDispersion2D
filename = "$GAMMAPY_DATA/hess-dl3-dr1/data/hess_dl3_dr1_obs_id_020136.fits.gz"
edisp = EnergyDispersion2D.read(filename, hdu="EDISP")
edisp.peek()
plt.show()
as a function of true energy (RMF)¶
EDispKernel instead represents an energy dispersion as a function of true energy only
(\(E_{\rm disp}(E| E_{\rm true})\) following the notation in IRF Theory).
EDispKernel contains the energy redistribution matrix (or redistribution matrix function, RMF,
in the OGIP standard). The energy redistribution provides the integral of the energy dispersion probability function over
bins of reconstructed energy. It is used to convert vectors of predicted counts in true energy in vectors of predicted
counts in reconstructed energy.
Its format specifications are available in RMF.
Such an energy dispersion can be obtained for example:
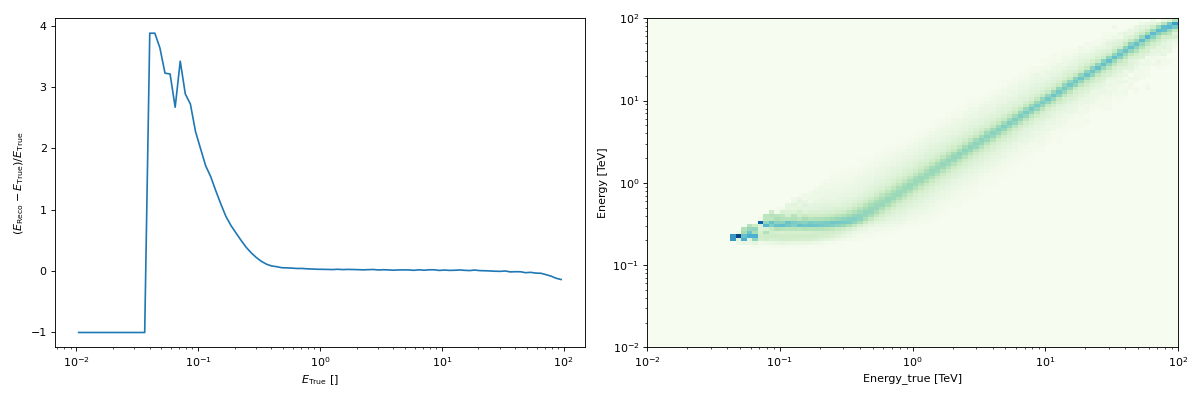
selecting the value of an
EnergyDispersion2Dat a given offset (usingAngle)
"""Plot the energy dispersion at a given offset."""
from astropy.coordinates import Angle
import matplotlib.pyplot as plt
from gammapy.irf import EnergyDispersion2D
filename = "$GAMMAPY_DATA/hess-dl3-dr1/data/hess_dl3_dr1_obs_id_020136.fits.gz"
edisp = EnergyDispersion2D.read(filename, hdu="EDISP")
# offset at which we want to examine the energy dispersion
offset = Angle("0.5 deg")
edisp_kernel = edisp.to_edisp_kernel(offset=offset)
edisp_kernel.peek()
plt.show()
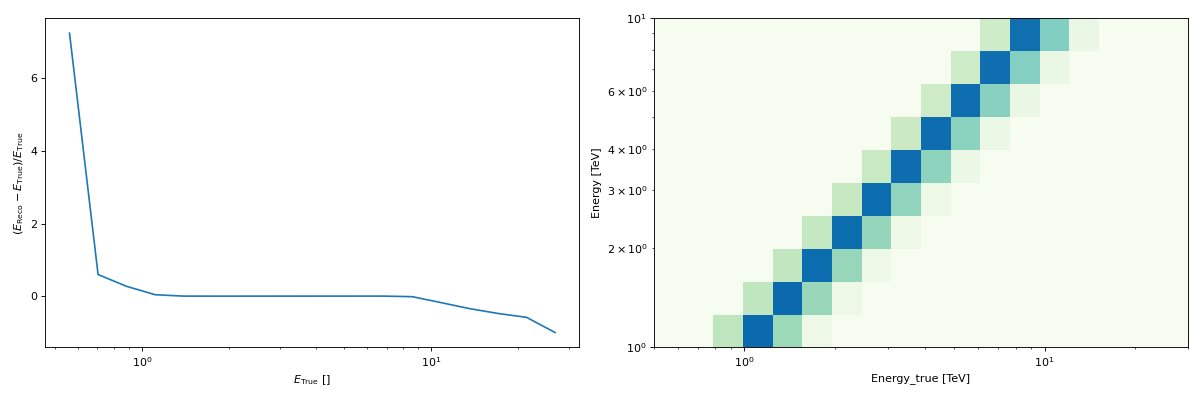
or starting from a parameterisation:
"""Plot an energy dispersion using a gaussian parametrisation"""
import matplotlib.pyplot as plt
from gammapy.irf import EDispKernel
from gammapy.maps import MapAxis
energy_axis = MapAxis.from_energy_bounds("1 TeV", "10 TeV", nbin=10)
energy_axis_true = MapAxis.from_energy_bounds(
"0.5 TeV", "30 TeV", nbin=10, per_decade=True, name="energy_true"
)
edisp = EDispKernel.from_gauss(
energy_axis=energy_axis, energy_axis_true=energy_axis_true, sigma=0.1, bias=0
)
edisp.peek()
plt.show()
Storing the energy dispersion information as a function of sky position¶
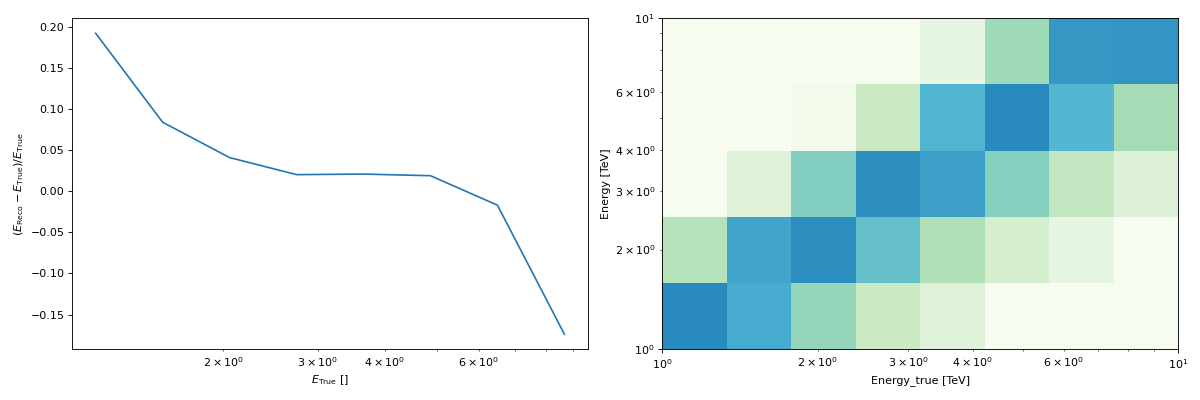
The gammapy.irf.EDispKernelMap is a four-dimensional Map that stores, for each position in the sky,
an EDispKernel, which, as described above, depends on true energy.
The EDispKernel at a given position can be extracted with get_edisp_kernel() by
providing a SkyCoord or SkyRegion.
from gammapy.irf import EDispKernelMap
from gammapy.maps import MapAxis
from astropy.coordinates import SkyCoord
# Create a test EDispKernelMap from a gaussian distribution
energy_axis_true = MapAxis.from_energy_bounds(1,10, 8, unit="TeV", name="energy_true")
energy_axis = MapAxis.from_energy_bounds(1,10, 5, unit="TeV", name="energy")
edisp_map = EDispKernelMap.from_gauss(energy_axis, energy_axis_true, 0.3, 0)
position = SkyCoord(ra=83, dec=22, unit='deg', frame='icrs')
edisp_kernel = edisp_map.get_edisp_kernel(position)
# We can quickly check the edisp kernel via the peek() method
edisp_kernel.peek()
The gammapy.irf.EDispMap serves a similar purpose but instead of a true energy axis,
it contains the information of the energy dispersion as a function of the energy migration (\(E/ E_{\rm true}\)).
It can be converted into a gammapy.irf.EDispKernelMap with gammapy.irf.EDispMap.to_edisp_kernel_map() and the
gammapy.irf.EDispKernelMap at a given position can be extracted in the same way as described above, using get_edisp_kernel()
and providing a SkyCoord.