This is a fixed-text formatted version of a Jupyter notebook

• Try online

• You may download all the notebooks in the documentation as a tar file.

• Source files: flux_profiles.ipynb | flux_profiles.py

Flux Profile Estimation

This tutorial shows how to estimate flux profiles.

Prerequisites

Knowledge of 3D data reduction and datasets used in Gammapy, see for instance the first analysis tutorial.

Context

A useful tool to study and compare the saptial distribution of flux in images and data cubes is the measurement of flxu profiles. Flux profiles can show spatial correlations of gamma-ray data with e.g. gas maps or other type of gamma-ray data. Most commonly flux profiles are measured along some preferred coordinate axis, either radially distance from a source of interest, along longitude and latitude coordinate axes or along the path defined by two spatial coordinates.

Proposed Approach

Flux profile estimation essentially works by estimating flux points for a set of predefined spatially connected regions. For radial flux profiles the shape of the regions are annuli with a common center, for linear profiles it’s typically a rectangular shape.

We will work on a pre-computed MapDataset of Fermi-LAT data, use Region to define the structure of the bins of the flux profile and run the actually profile extraction using the FluxProfileEstimator

Setup and Imports

%matplotlib inline
import matplotlib.pyplot as plt
from astropy import units as u
from astropy.coordinates import SkyCoord
import numpy as np

from gammapy.datasets import MapDataset
from gammapy.estimators import FluxProfileEstimator, FluxPoints
from gammapy.maps import RegionGeom
from gammapy.utils.regions import (
    make_concentric_annulus_sky_regions,
    make_orthogonal_rectangle_sky_regions,
)
from gammapy.modeling.models import PowerLawSpectralModel

Read and Introduce Data

dataset = MapDataset.read(
    "$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc.fits.gz", name="fermi-dataset"
)

This is what the counts image we will work with looks like:

counts_image = dataset.counts.sum_over_axes()
counts_image.smooth("0.1 deg").plot(stretch="sqrt");

There are 400x200 pixels in the dataset and 11 energy bins between 10 GeV and 2 TeV:

print(dataset.counts)

WcsNDMap

        geom  : WcsGeom
        axes  : ['lon', 'lat', 'energy']
        shape : (400, 200, 11)
        ndim  : 3
        unit  :
        dtype : >i4

Profile Estimation

Configuration

We start by defining a list of spatially connected regions along the galactic longitude axis. For this there is a helper function make_orthogonal_rectangle_sky_regions. The individual region bins for the profile have a height of 3 deg and in total there are 31 bins. The starts from lon = 10 deg tand goes to lon = 350 deg. In addition we have to specify the wcs to take into account possible projections effects on the region definition:

regions = make_orthogonal_rectangle_sky_regions(
    start_pos=SkyCoord("10d", "0d", frame="galactic"),
    end_pos=SkyCoord("350d", "0d", frame="galactic"),
    wcs=counts_image.geom.wcs,
    height="3 deg",
    nbin=51,
)

We can use the RegionGeom object to illustrate the regions on top of the counts image:

geom = RegionGeom.create(region=regions)
ax = counts_image.smooth("0.1 deg").plot(stretch="sqrt")
geom.plot_region(ax=ax, color="w");

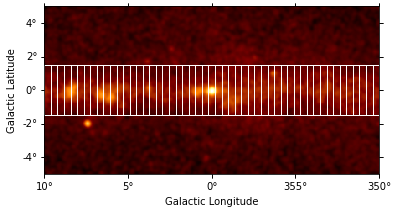
Next we create the FluxProfileEstimator. For the estimation of the flux profile we assume a spectral model with a power-law shape and an index of 2.3

flux_profile_estimator = FluxProfileEstimator(
    regions=regions,
    spectrum=PowerLawSpectralModel(index=2.3),
    energy_edges=[10, 2000] * u.GeV,
    selection_optional=["ul"],
)

We can see the full configuration by printing the estimator object:

print(flux_profile_estimator)

FluxProfileEstimator
--------------------

  energy_edges           : [  10. 2000.] GeV
  fit                    : <gammapy.modeling.fit.Fit object at 0x13f9adf40>
  n_sigma                : 1
  n_sigma_ul             : 2
  norm_max               : 5
  norm_min               : 0.2
  norm_n_values          : 11
  norm_values            : None
  null_value             : 0
  reoptimize             : False
  selection_optional     : ['ul']
  source                 : 0
  spectrum               : PowerLawSpectralModel
  sum_over_energy_groups : False

Run Estimation

Now we can run the profile estimation and explore the results:

%%time
profile = flux_profile_estimator.run(datasets=dataset)

CPU times: user 6.87 s, sys: 121 ms, total: 6.99 s
Wall time: 6.76 s

print(profile)

FluxPoints
----------

  geom                   : RegionGeom
  axes                   : ['lon', 'lat', 'energy', 'projected-distance']
  shape                  : (1, 1, 1, 51)
  quantities             : ['norm', 'norm_err', 'norm_ul', 'ts', 'npred', 'npred_excess', 'stat', 'counts', 'success']
  ref. model             : pl
  n_sigma                : 1
  n_sigma_ul             : 2
  sqrt_ts_threshold_ul   : 2
  sed type init          : likelihood

We can see the flux profile is represented by a FluxPoints object with a projected-distance axis, which defines the main axis the flux profile is measured along. The lon and lat axes can be ignored.

Plotting Results

Let us directly plot the result using FluxPoints.plot():

ax = profile.plot(sed_type="dnde")
ax.set_yscale("linear")

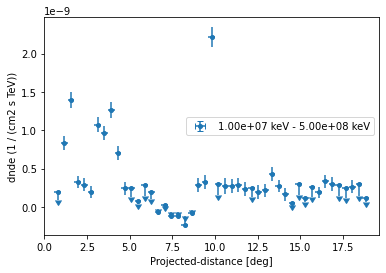
Based on the spectral model we specified above we can also plot in any other sed type, e.g. energy flux and define a different threshold when to plot upper limits:

profile.sqrt_ts_threshold_ul = 2

ax = profile.plot(sed_type="eflux")
ax.set_yscale("linear")

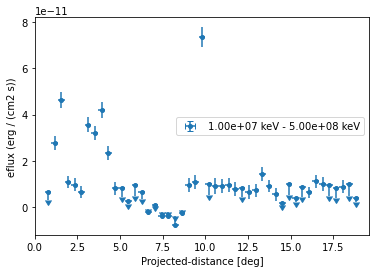
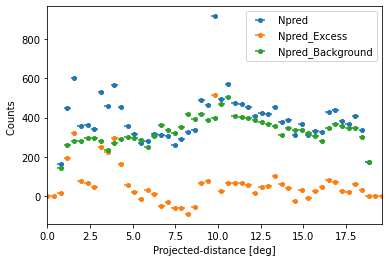
We can also plot any other quantity of interest, that is defined on the FluxPoints result object. E.g. the predicted total counts, background counts and excess counts:

quantities = ["npred", "npred_excess", "npred_background"]

for quantity in quantities:
    profile[quantity].plot(label=quantity.title())

plt.ylabel("Counts ")

Text(0, 0.5, 'Counts ')

Serialisation and I/O

The profile can be serialised using FluxPoints.write(), given a specific format:

profile.write(
    filename="flux_profile_fermi.fits",
    format="profile",
    overwrite=True,
    sed_type="dnde",
)

profile_new = FluxPoints.read(
    filename="flux_profile_fermi.fits", format="profile"
)

No reference model set for FluxMaps. Assuming point source with E^-2 spectrum.

ax = profile_new.plot()
ax.set_yscale("linear")

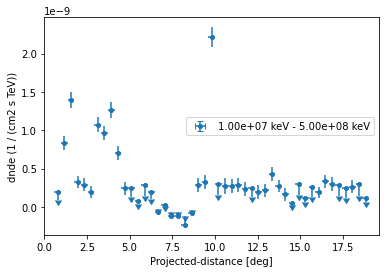
The profile can be serialised to a ~astropy.table.Table object using:

table = profile.to_table(format="profile", formatted=True)
table

Table length=51

x_min	x_max	x_ref	e_ref [1]	e_min [1]	e_max [1]	ref_dnde [1]	ref_flux [1]	ref_eflux [1]	norm [1]	norm_err [1]	norm_ul [1]	ts [1]	sqrt_ts [1]	npred [1,1]	npred_excess [1,1]	stat [1]	is_ul [1]	counts [1,1]	success [1]
deg	deg	deg	keV	keV	keV	1 / (cm2 s TeV)	keV / (cm2 s TeV)	keV2 / (cm2 s TeV)
float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float32	float64	bool	float64	bool
-0.1960784313725492	0.1960784313725492	0.0	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	nan	nan	nan	nan	nan	nan	0.0	0.000	False	0.0	False
0.1960784313725492	0.5882352941176467	0.392156862745098	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	nan	nan	nan	nan	nan	nan	0.0	0.000	False	0.0	False
0.5882352941176467	0.9803921568627443	0.7843137254901955	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.172	0.124	0.434	2.059	1.435	162.23048986115955	17.448376	-818.848	True	163.0	True
0.9803921568627443	1.3725490196078436	1.176470588235294	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	1.894	0.207	2.322	120.591	10.981	450.20181889217974	192.60909	-3013.446	False	448.0	True
1.3725490196078436	1.764705882352942	1.5686274509803928	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	3.146	0.240	3.639	280.648	16.753	601.6822045016994	320.15994	-4348.966	False	599.0	True
1.764705882352942	2.15686274509804	1.960784313725491	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.736	0.183	1.116	18.991	4.358	357.6650304886396	74.95968	-2218.623	False	354.0	True
2.15686274509804	2.549019607843138	2.3529411764705888	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.656	0.186	1.042	14.214	3.770	363.83338136609376	66.89659	-2452.717	False	367.0	True
2.549019607843138	2.941176470588236	2.745098039215687	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.450	0.179	0.821	7.011	2.648	339.4818273314676	45.943058	-2174.005	False	339.0	True
2.941176470588236	3.3333333333333344	3.137254901960785	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	2.421	0.225	2.885	174.146	13.196	528.0599574489612	247.276	-3887.531	False	531.0	True
3.3333333333333344	3.725490196078432	3.529411764705883	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	2.190	0.209	2.621	169.698	13.027	457.3561643542095	223.84384	-3183.973	False	458.0	True
3.725490196078432	4.117647058823529	3.9215686274509807	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	2.868	0.232	3.345	243.821	15.615	564.4775740614491	293.2505	-4201.048	False	566.0	True
4.117647058823529	4.509803921568627	4.313725490196078	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	1.599	0.205	2.023	81.901	9.050	451.76273200537855	163.63295	-3040.782	False	448.0	True
4.509803921568627	4.901960784313727	4.7058823529411775	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.550	0.182	0.928	10.243	3.201	356.28517250965956	56.336945	-2313.852	False	356.0	True
4.901960784313727	5.294117647058824	5.098039215686276	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.210	0.171	0.566	1.586	1.259	315.49805616415784	21.543198	-1979.035	True	315.0	True
5.294117647058824	5.686274509803923	5.4901960784313735	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	-0.147	0.159	0.184	0.824	-0.908	271.28752712430287	-15.065349	-1643.463	True	272.0	True
5.686274509803923	6.07843137254902	5.882352941176471	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.302	0.162	0.640	3.766	1.941	282.32873883100837	31.023876	-1692.050	True	282.0	True
6.07843137254902	6.470588235294118	6.274509803921569	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.093	0.172	0.451	0.301	0.549	317.7330763355026	9.594112	-2034.334	True	319.0	True
6.470588235294118	6.862745098039216	6.666666666666667	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	-0.500	0.170	-0.147	7.804	-2.794	311.3167047326352	-51.37142	-1931.193	True	311.0	True
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
12.352941176470619	12.745098039215696	12.549019607843157	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.441	0.197	0.848	5.381	2.320	424.9721062687647	45.757168	-2877.351	False	425.0	True
12.745098039215696	13.137254901960773	12.941176470588236	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.492	0.194	0.893	7.018	2.649	416.7588470906105	51.088707	-2705.136	False	412.0	True
13.137254901960773	13.529411764705875	13.333333333333325	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.959	0.205	1.382	25.879	5.087	455.22507305193835	99.72924	-3216.032	False	458.0	True
13.529411764705875	13.921568627451002	13.72549019607844	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.611	0.184	0.993	12.465	3.531	376.66733293729885	63.567978	-2403.516	False	373.0	True
13.921568627451002	14.31372549019608	14.117647058823541	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.377	0.187	0.763	4.407	2.099	385.1566764851361	39.272778	-2526.278	False	384.0	True
14.31372549019608	14.705882352941185	14.509803921568633	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	-0.244	0.168	0.103	2.022	-1.422	313.3736443463295	-25.44988	-1936.261	True	313.0	True
14.705882352941185	15.098039215686311	14.901960784313747	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.307	0.179	0.679	3.133	1.770	366.322547445814	32.01158	-2178.012	True	357.0	True
15.098039215686311	15.490196078431389	15.294117647058851	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	-0.083	0.167	0.265	0.240	-0.490	313.4101919680869	-8.618814	-1914.901	True	311.0	True
15.490196078431389	15.882352941176466	15.686274509803926	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.228	0.172	0.584	1.863	1.365	330.89113194006126	23.80037	-2016.119	True	327.0	True
15.882352941176466	16.274509803921596	16.07843137254903	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.427	0.170	0.780	6.979	2.642	324.69019708074285	44.554733	-1957.576	False	321.0	True
16.274509803921596	16.666666666666696	16.470588235294144	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.760	0.195	1.163	17.553	4.190	428.005206597181	79.45124	-2767.621	False	421.0	True
16.666666666666696	17.058823529411775	16.862745098039234	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.675	0.197	1.082	13.277	3.644	437.13415063137586	70.588745	-2830.574	False	431.0	True
17.058823529411775	17.4509803921569	17.254901960784338	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.256	0.183	0.634	2.057	1.434	381.24750962187824	26.727816	-2356.744	True	374.0	True
17.4509803921569	17.843137254902004	17.647058823529452	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.174	0.182	0.551	0.951	0.975	366.45334911783	18.242867	-2463.364	True	370.0	True
17.843137254902004	18.235294117647083	18.039215686274545	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.593	0.192	0.990	10.705	3.272	408.05504964497743	62.12828	-2803.387	False	410.0	True
18.235294117647083	18.627450980392158	18.43137254901962	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.306	0.173	0.666	3.342	1.828	334.14141424669504	32.074398	-2186.572	True	336.0	True
18.627450980392158	19.01960784313726	18.82352941176471	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	0.010	0.124	0.269	0.005	0.071	171.8115649139593	0.9959075	-877.032	True	172.0	True
19.01960784313726	19.41176470588239	19.215686274509824	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	nan	nan	nan	nan	nan	nan	0.0	0.000	False	0.0	False
19.41176470588239	19.803921568627494	19.607843137254942	70710678.119	10000000.000	500000000.000	4.428e-10	3.043e-01	9.166e+06	nan	nan	nan	nan	nan	nan	0.0	0.000	False	0.0	False

No we can also estimate a radial profile starting from the Galactic center:

regions = make_concentric_annulus_sky_regions(
    center=SkyCoord("0d", "0d", frame="galactic"),
    radius_max="1.5 deg",
    nbin=11,
)

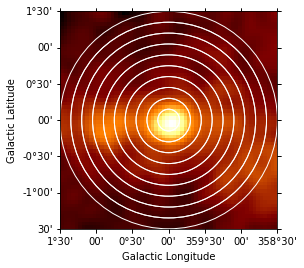
Again we first illustrate the regions:

geom = RegionGeom.create(region=regions)
gc_image = counts_image.cutout(
    position=SkyCoord("0d", "0d", frame="galactic"), width=3 * u.deg
)
ax = gc_image.smooth("0.1 deg").plot(stretch="sqrt")
geom.plot_region(ax=ax, color="w");

/Users/adonath/software/mambaforge/envs/gammapy-dev/lib/python3.9/site-packages/scipy/optimize/_numdiff.py:579: RuntimeWarning: invalid value encountered in true_divide
  J_transposed[i] = df / dx

This time we define two energy bins and include the fit statistic profile in the computation:

flux_profile_estimator = FluxProfileEstimator(
    regions=regions,
    spectrum=PowerLawSpectralModel(index=2.3),
    energy_edges=[10, 100, 2000] * u.GeV,
    selection_optional=["ul", "scan"],
    norm_values=np.linspace(-1, 5, 11),
)

profile = flux_profile_estimator.run(datasets=dataset)

We can directly plot the result:

ax = profile.plot(axis_name="projected-distance", sed_type="flux")

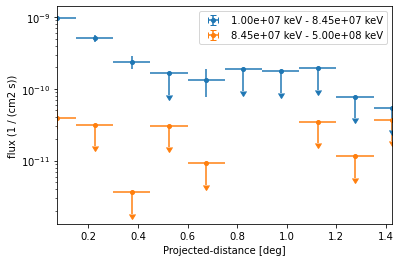
However because of the powerlaw spectrum the flux at high energies is much lower. To extract the profile at high energies only we can use:

profile_high = profile.slice_by_idx({"energy": slice(1, 2)})

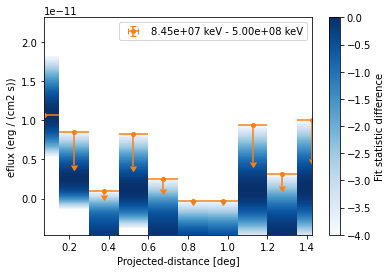
And now plot the points together with the likelihood profiles:

ax = profile_high.plot(sed_type="eflux", color="tab:orange")
profile_high.plot_ts_profiles(ax=ax, sed_type="eflux")
ax.set_yscale("linear")