This is a fixed-text formatted version of a Jupyter notebook

Try online
You may download all the notebooks in the documentation as a tar file.
Source files: light_curve_simulation.ipynb | light_curve_simulation.py

Simulating and fitting a time varying source¶

Prerequisites:¶

To understand how a single binned simulation works, please refer to spectrum_simulation simulate_3d for 1D and 3D simulations respectively.
For details of light curve extraction using gammapy, refer to the two tutorials light_curve and light_curve_flare

Context¶

Frequently, studies of variable sources (eg: decaying GRB light curves, AGN flares, etc) require time variable simulations. For most use cases, generating an event list is an overkill, and it suffices to use binned simulations using a temporal model.

Objective: Simulate and fit a time decaying light curve of a source with CTA using the CTA 1DC response

Proposed approach:¶

We will simulate 10 spectral datasets within given time intervals (Good Time Intervals) following a given spectral (a power law) and temporal profile (an exponential decay, with a decay time of 6 hr ). These are then analysed using the light curve estimator to obtain flux points. Then, we re-fit the simulated datasets to reconstruct back the injected profiles.

In summary, necessary steps are:

Choose observation parameters including a list of gammapy.data.GTI
Define temporal and spectral models from :ref:model-gallery as per science case
Perform the simulation (in 1D or 3D)
Extract the light curve from the reduced dataset as shown in light curve notebook
Optionally, we show here how to fit the simulated datasets using a source model

Setup¶

As usual, we’ll start with some general imports…

Setup¶

[1]:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from astropy.time import Time

import logging

log = logging.getLogger(__name__)

And some gammapy specific imports

[2]:

from gammapy.data import Observation
from gammapy.irf import load_cta_irfs
from gammapy.datasets import SpectrumDataset, Datasets
from gammapy.modeling.models import (
    PowerLawSpectralModel,
    ExpDecayTemporalModel,
    SkyModel,
)
from gammapy.maps import MapAxis, RegionGeom
from gammapy.estimators import LightCurveEstimator
from gammapy.makers import SpectrumDatasetMaker
from gammapy.modeling import Fit

Simulating a light curve¶

We will simulate 10 datasets using an PowerLawSpectralModel and a ExpDecayTemporalModel. The important thing to note here is how to attach a different GTI to each dataset.

[3]:

# Loading IRFs
irfs = load_cta_irfs(
    "$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)

Invalid unit found in background table! Assuming (s-1 MeV-1 sr-1)

[4]:

# Reconstructed and true energy axis
energy_axis = MapAxis.from_edges(
    np.logspace(-0.5, 1.0, 10), unit="TeV", name="energy", interp="log"
)
energy_axis_true = MapAxis.from_edges(
    np.logspace(-1.2, 2.0, 31), unit="TeV", name="energy_true", interp="log"
)

geom = RegionGeom.create("galactic;circle(0, 0, 0.11)", axes=[energy_axis])

[5]:

# Pointing position
pointing = SkyCoord(0.5, 0.5, unit="deg", frame="galactic")

Note that observations are usually conducted in Wobble mode, in which the source is not in the center of the camera. This allows to have a symmetrical sky position from which background can be estimated.

[6]:

# Define the source model: A combination of spectral and temporal model

gti_t0 = Time("2020-03-01")
spectral_model = PowerLawSpectralModel(
    index=3, amplitude="1e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)
temporal_model = ExpDecayTemporalModel(t0="6 h", t_ref=gti_t0.mjd * u.d)

model_simu = SkyModel(
    spectral_model=spectral_model,
    temporal_model=temporal_model,
    name="model-simu",
)

/Users/adonath/software/mambaforge/envs/gammapy-dev/lib/python3.9/site-packages/astropy/units/quantity.py:486: RuntimeWarning: overflow encountered in exp
  result = super().__array_ufunc__(function, method, *arrays, **kwargs)
/Users/adonath/software/mambaforge/envs/gammapy-dev/lib/python3.9/site-packages/astropy/units/quantity.py:486: RuntimeWarning: invalid value encountered in subtract
  result = super().__array_ufunc__(function, method, *arrays, **kwargs)

[7]:

# Look at the model
model_simu.parameters.to_table()

[7]:

Table length=5

type	name	value	unit	error	min	max	frozen	link
str8	str9	float64	str14	int64	float64	float64	bool	str1
spectral	index	3.0000e+00		0.000e+00	nan	nan	False
spectral	amplitude	1.0000e-11	cm-2 s-1 TeV-1	0.000e+00	nan	nan	False
spectral	reference	1.0000e+00	TeV	0.000e+00	nan	nan	True
temporal	t0	6.0000e+00	h	0.000e+00	nan	nan	False
temporal	t_ref	5.8909e+04	d	0.000e+00	nan	nan	True

Now, define the start and observation livetime wrt to the reference time, gti_t0

[8]:

n_obs = 10
tstart = [1, 2, 3, 5, 8, 10, 20, 22, 23, 24] * u.h
lvtm = [55, 25, 26, 40, 40, 50, 40, 52, 43, 47] * u.min

Now perform the simulations

[9]:

datasets = Datasets()

empty = SpectrumDataset.create(
    geom=geom, energy_axis_true=energy_axis_true, name="empty"
)

maker = SpectrumDatasetMaker(selection=["exposure", "background", "edisp"])

for idx in range(n_obs):
    obs = Observation.create(
        pointing=pointing,
        livetime=lvtm[idx],
        tstart=tstart[idx],
        irfs=irfs,
        reference_time=gti_t0,
        obs_id=idx,
    )
    empty_i = empty.copy(name=f"dataset-{idx}")
    dataset = maker.run(empty_i, obs)
    dataset.models = model_simu
    dataset.fake()
    datasets.append(dataset)

The reduced datasets have been successfully simulated. Let’s take a quick look into our datasets.

[10]:

datasets.info_table()

[10]:

Table length=10

name	counts	background	excess	sqrt_ts	npred	npred_background	npred_signal	exposure_min	exposure_max	livetime	ontime	counts_rate	background_rate	excess_rate	n_bins	n_fit_bins	stat_type	stat_sum
								m2 s	m2 s	s	s	1 / s	1 / s	1 / s
str9	int64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	float64	int64	int64	str4	float64
stacked	838	20.318769454956055	817.6812133789062	67.81205166098117	20.318769738078117	20.318769454956055	nan	216137904.0	16025275392.0	3299.999999999999	3300.0	0.253939393939394	0.0061572028651382	0.2477821858723959	9	9	cash	nan
dataset-1	335	9.235804207223003	325.764195792777	41.88639768268303	332.14961280987876	9.235804207223003	322.91380860265576	98244500.93556339	7284216297.312269	1500.0	1500.0	0.22333333333333333	0.0061572028048153355	0.217176130528518	9	9	cash	-2096.519112853783
dataset-2	319	9.605236375511922	309.39476362448806	40.20011982055861	293.4896025844928	9.605236375511922	283.88436620898085	102174280.97298592	7575584949.20476	1560.0	1560.0	0.20448717948717948	0.006157202804815335	0.19832997668236416	9	9	cash	-1999.167487932759
dataset-3	331	14.777286731556805	316.2227132684432	37.75884642088334	321.7838594188438	14.777286731556805	307.006572687287	157191201.49690142	11654746075.69963	2400.0	2400.0	0.13791666666666666	0.0061572028048153355	0.13175946386185133	9	9	cash	-2093.961371303704
dataset-4	191	14.777286731556783	176.22271326844321	25.003242551912294	200.98618579969124	14.777286731556783	186.20889906813449	157191201.49690118	11654746075.699614	2399.9999999999964	2399.9999999999964	0.07958333333333345	0.0061572028048153355	0.07342613052851812	9	9	cash	-950.0232173832845
dataset-5	156	18.471608414446006	137.528391585554	19.764438032194874	182.9994427293594	18.471608414446006	164.52783431491338	196489001.87112677	14568432594.624538	3000.0	3000.0	0.052	0.0061572028048153355	0.04584279719518467	9	9	cash	-679.5591099561027
dataset-6	37	14.777286731556805	22.222713268443194	4.8449707117063845	39.97792082812076	14.777286731556805	25.200634096563952	157191201.49690142	11654746075.69963	2400.0	2400.0	0.015416666666666667	0.0061572028048153355	0.00925946386185133	9	9	cash	-83.5158051456156
dataset-7	34	19.210472751023843	14.789527248976157	3.0401449505762996	42.30482881205312	19.210472751023843	23.094356061029266	204348561.94597185	15151169898.40952	3120.0	3120.0	0.010897435897435897	0.006157202804815335	0.004740233092620563	9	9	cash	-70.91103544138612
dataset-8	31	15.885583236423564	15.114416763576436	3.3500492819057928	32.24990050265124	15.885583236423564	16.36431726622769	168980541.609169	12528852031.377102	2580.0	2580.0	0.012015503875968992	0.006157202804815335	0.005858301071153657	9	9	cash	-42.09535699583043
dataset-9	41	17.363311909579245	23.636688090420755	4.814774845348613	32.421835197092264	17.363311909579245	15.058523287513015	184699661.75885916	13694326638.947065	2820.0	2820.0	0.014539007092198582	0.0061572028048153355	0.008381804287383247	9	9	cash	-96.29813771797772

Extract the lightcurve¶

This section uses standard light curve estimation tools for a 1D extraction. Only a spectral model needs to be defined in this case. Since the estimator returns the integrated flux separately for each time bin, the temporal model need not be accounted for at this stage.

[11]:

# Define the model:
spectral_model = PowerLawSpectralModel(
    index=3, amplitude="1e-11 cm-2 s-1 TeV-1", reference="1 TeV"
)
model_fit = SkyModel(spectral_model=spectral_model, name="model-fit")

[12]:

# Attach model to all datasets
datasets.models = model_fit

[13]:

%%time
lc_maker_1d = LightCurveEstimator(
    energy_edges=[0.3, 10] * u.TeV,
    source="model-fit",
    selection_optional=["ul"],
)
lc_1d = lc_maker_1d.run(datasets)

CPU times: user 1.45 s, sys: 18.5 ms, total: 1.47 s
Wall time: 1.47 s

[14]:

ax = lc_1d.plot(marker="o", label="3D")

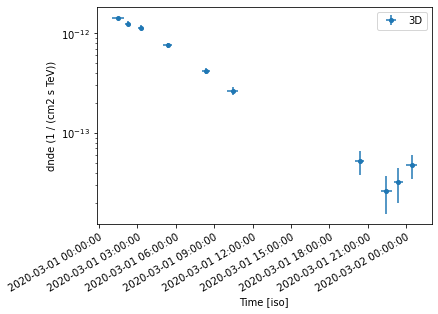
../../../_images/tutorials_analysis_time_light_curve_simulation_23_0.png

We have the reconstructed lightcurve at this point. Further standard analysis might involve modeling the temporal profiles with an analytical or theoretical model. You may do this using your favourite fitting package, one possible option being curve_fit inside scipy.optimize.

In the next section, we show how to simultaneously fit the all datasets using a given temporal model. This does a joint fitting across the different datasets, while simultaneously minimising across the temporal model parameters as well. We will fit the amplitude, spectral index and the decay time scale. Note that t_ref should be fixed by default for the ExpDecayTemporalModel.

For modelling and fitting more complex flares, you should attach the relevant model to each group of datasets. The parameters of a model in a given group of dataset will be tied. For more details on joint fitting in gammapy, see here.

Fit the datasets¶

[15]:

# Define the model:
spectral_model1 = PowerLawSpectralModel(
    index=2.0, amplitude="1e-12 cm-2 s-1 TeV-1", reference="1 TeV"
)
temporal_model1 = ExpDecayTemporalModel(t0="10 h", t_ref=gti_t0.mjd * u.d)

model = SkyModel(
    spectral_model=spectral_model1,
    temporal_model=temporal_model1,
    name="model-test",
)

/Users/adonath/software/mambaforge/envs/gammapy-dev/lib/python3.9/site-packages/astropy/units/quantity.py:486: RuntimeWarning: overflow encountered in exp
  result = super().__array_ufunc__(function, method, *arrays, **kwargs)
/Users/adonath/software/mambaforge/envs/gammapy-dev/lib/python3.9/site-packages/astropy/units/quantity.py:486: RuntimeWarning: invalid value encountered in subtract
  result = super().__array_ufunc__(function, method, *arrays, **kwargs)

[16]:

model.parameters.to_table()

[16]:

Table length=5

type	name	value	unit	error	min	max	frozen	link
str8	str9	float64	str14	int64	float64	float64	bool	str1
spectral	index	2.0000e+00		0.000e+00	nan	nan	False
spectral	amplitude	1.0000e-12	cm-2 s-1 TeV-1	0.000e+00	nan	nan	False
spectral	reference	1.0000e+00	TeV	0.000e+00	nan	nan	True
temporal	t0	1.0000e+01	h	0.000e+00	nan	nan	False
temporal	t_ref	5.8909e+04	d	0.000e+00	nan	nan	True

[17]:

datasets.models = model

[18]:

%%time
# Do a joint fit
fit = Fit()
result = fit.run(datasets=datasets)

CPU times: user 3.22 s, sys: 41.5 ms, total: 3.26 s
Wall time: 3.23 s

[19]:

result.parameters.to_table()

[19]:

Table length=5

type	name	value	unit	error	min	max	frozen	link
str8	str9	float64	str14	float64	float64	float64	bool	str1
spectral	index	2.9693e+00		3.133e-02	nan	nan	False
spectral	amplitude	1.0603e-11	cm-2 s-1 TeV-1	3.703e-13	nan	nan	False
spectral	reference	1.0000e+00	TeV	0.000e+00	nan	nan	True
temporal	t0	5.6466e+00	h	1.982e-01	nan	nan	False
temporal	t_ref	5.8909e+04	d	0.000e+00	nan	nan	True

We see that the fitted parameters match well with the simulated ones!

Exercises¶

Re-do the analysis with MapDataset instead of SpectralDataset
Model the flare of PKS 2155-304 which you obtained using the light curve flare tutorial. Use a combination of a Gaussian and Exponential flare profiles, and fit using scipy.optimize.curve_fit
Do a joint fitting of the datasets.

[ ]: