Dark matter spatial and spectral models

Convenience methods for dark matter high level analyses.

Introduction

Gammapy has some convenience methods for dark matter analyses in darkmatter. These include J-Factor computation and calculation the expected gamma flux for a number of annihilation channels. They are presented in this notebook.

The basic concepts of indirect dark matter searches, however, are not explained. So this is aimed at people who already know what the want to do. A good introduction to indirect dark matter searches is given for example in https://arxiv.org/pdf/1012.4515.pdf (Chapter 1 and 5)

Setup

As always, we start with some setup for the notebook, and with imports.

import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from regions import CircleSkyRegion, RectangleSkyRegion

# %matplotlib inline
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from gammapy.astro.darkmatter import (
    DarkMatterAnnihilationSpectralModel,
    DarkMatterDecaySpectralModel,
    JFactory,
    PrimaryFlux,
    profiles,
)
from gammapy.maps import WcsGeom, WcsNDMap

Check setup

from gammapy.utils.check import check_tutorials_setup

check_tutorials_setup()

System:

        python_executable      : /home/runner/work/gammapy-docs/gammapy-docs/gammapy/.tox/build_docs/bin/python
        python_version         : 3.9.20
        machine                : x86_64
        system                 : Linux


Gammapy package:

        version                : 2.0.dev105+g0726d256d
        path                   : /home/runner/work/gammapy-docs/gammapy-docs/gammapy/.tox/build_docs/lib/python3.9/site-packages/gammapy


Other packages:

        numpy                  : 1.26.4
        scipy                  : 1.13.1
        astropy                : 5.2.2
        regions                : 0.8
        click                  : 8.1.7
        yaml                   : 6.0.2
        IPython                : 8.18.1
        jupyterlab             : not installed
        matplotlib             : 3.9.3
        pandas                 : not installed
        healpy                 : 1.17.3
        iminuit                : 2.30.1
        sherpa                 : 4.16.1
        naima                  : 0.10.0
        emcee                  : 3.1.6
        corner                 : 2.2.3
        ray                    : 2.39.0


Gammapy environment variables:

        GAMMAPY_DATA           : /home/runner/work/gammapy-docs/gammapy-docs/gammapy-datasets/dev

Profiles

The following dark matter profiles are currently implemented. Each model can be scaled to a given density at a certain distance. These parameters are controlled by LOCAL_DENSITY and DISTANCE_GC

profiles.DMProfile.__subclasses__()

for profile in profiles.DMProfile.__subclasses__():
    p = profile()
    p.scale_to_local_density()
    radii = np.logspace(-3, 2, 100) * u.kpc
    plt.plot(radii, p(radii), label=p.__class__.__name__)

plt.loglog()
plt.axvline(8.5, linestyle="dashed", color="black", label="local density")
plt.legend()
plt.show()

print("LOCAL_DENSITY:", profiles.DMProfile.LOCAL_DENSITY)
print("DISTANCE_GC:", profiles.DMProfile.DISTANCE_GC)

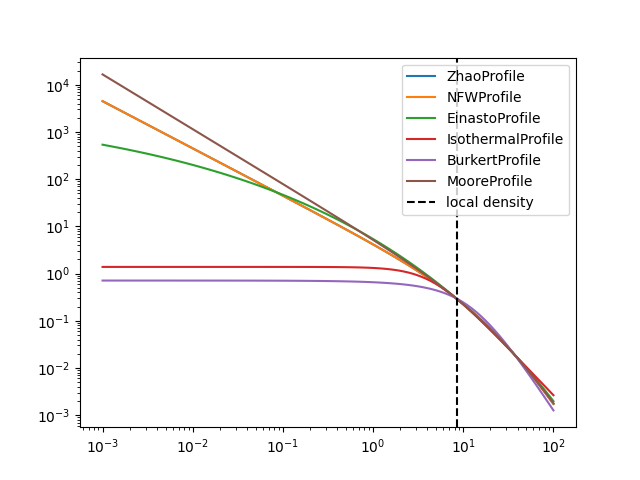
LOCAL_DENSITY: 0.3 GeV / cm3
DISTANCE_GC: 8.33 kpc

J Factors

There are utilities to compute J-Factor maps that can serve as a basis to compute J-Factors for certain regions. In the following we compute a J-Factor annihilation map for the Galactic Centre region

profile = profiles.NFWProfile(r_s=20 * u.kpc)

# Adopt standard values used in H.E.S.S.
profiles.DMProfile.DISTANCE_GC = 8.5 * u.kpc
profiles.DMProfile.LOCAL_DENSITY = 0.39 * u.Unit("GeV / cm3")

profile.scale_to_local_density()

position = SkyCoord(0.0, 0.0, frame="galactic", unit="deg")
geom = WcsGeom.create(binsz=0.05, skydir=position, width=3.0, frame="galactic")

jfactory = JFactory(geom=geom, profile=profile, distance=profiles.DMProfile.DISTANCE_GC)
jfact = jfactory.compute_jfactor()

jfact_map = WcsNDMap(geom=geom, data=jfact.value, unit=jfact.unit)
plt.figure()
ax = jfact_map.plot(cmap="viridis", norm=LogNorm(), add_cbar=True)
plt.title(f"J-Factor [{jfact_map.unit}]")

# 1 deg circle usually used in H.E.S.S. analyses without the +/- 0.3 deg band around the plane
sky_reg = CircleSkyRegion(center=position, radius=1 * u.deg)
pix_reg = sky_reg.to_pixel(wcs=geom.wcs)
pix_reg.plot(ax=ax, facecolor="none", edgecolor="red", label="1 deg circle")

sky_reg_rec = RectangleSkyRegion(center=position, height=0.6 * u.deg, width=2 * u.deg)
pix_reg_rec = sky_reg_rec.to_pixel(wcs=geom.wcs)
pix_reg_rec.plot(ax=ax, facecolor="none", edgecolor="orange", label="+/- 0.3 deg band")

plt.legend()
plt.show()

# NOTE: https://arxiv.org/abs/1607.08142 quote 2.67e21
total_jfact = (
    pix_reg.to_mask().multiply(jfact).sum()
    - pix_reg_rec.to_mask().multiply(jfact).sum()
)
total_jfact = (
    pix_reg.to_mask().multiply(jfact).sum()
    - pix_reg_rec.to_mask().multiply(jfact).sum()
)
print(
    "J-factor in 1 deg circle without the +/- 0.3 deg band around GC assuming a "
    f"{profile.__class__.__name__} is {total_jfact:.3g}"
)

J-factor in 1 deg circle without the +/- 0.3 deg band around GC assuming a NFWProfile is 2.36e+21 GeV2 / cm5

The J-Factor can also be computed for dark matter decay

jfactory = JFactory(
    geom=geom,
    profile=profile,
    distance=profiles.DMProfile.DISTANCE_GC,
    annihilation=False,
)
jfact_decay = jfactory.compute_jfactor()

jfact_map = WcsNDMap(geom=geom, data=jfact_decay.value, unit=jfact_decay.unit)
plt.figure()
ax = jfact_map.plot(cmap="viridis", norm=LogNorm(), add_cbar=True)
plt.title(f"J-Factor [{jfact_map.unit}]")

# 1 deg circle usually used in H.E.S.S. analyses without the +/- 0.3 deg band around the plane
sky_reg = CircleSkyRegion(center=position, radius=1 * u.deg)
pix_reg = sky_reg.to_pixel(wcs=geom.wcs)
pix_reg.plot(ax=ax, facecolor="none", edgecolor="red", label="1 deg circle")

sky_reg_rec = RectangleSkyRegion(center=position, height=0.6 * u.deg, width=2 * u.deg)
pix_reg_rec = sky_reg_rec.to_pixel(wcs=geom.wcs)
pix_reg_rec.plot(ax=ax, facecolor="none", edgecolor="orange", label="+/- 0.3 deg band")

plt.legend()
plt.show()

total_jfact_decay = (
    pix_reg.to_mask().multiply(jfact_decay).sum()
    - pix_reg_rec.to_mask().multiply(jfact_decay).sum()
)
total_jfact_decay = (
    pix_reg.to_mask().multiply(jfact_decay).sum()
    - pix_reg_rec.to_mask().multiply(jfact_decay).sum()
)
print(
    "J-factor in 1 deg circle without the +/- 0.3 deg band around GC assuming a "
    f"{profile.__class__.__name__} is {total_jfact_decay:.3g}"
)

J-factor in 1 deg circle without the +/- 0.3 deg band around GC assuming a NFWProfile is 1.14e+20 GeV / cm2

Gamma-ray spectra at production

The gamma-ray spectrum per annihilation is a further ingredient for a dark matter analysis. The following annihilation channels are supported. For more info see https://arxiv.org/pdf/1012.4515.pdf

fluxes = PrimaryFlux(mDM="1 TeV", channel="eL")
print(fluxes.allowed_channels)

fig, axes = plt.subplots(4, 1, figsize=(4, 16))
mDMs = [0.01, 0.1, 1, 10] * u.TeV

for mDM, ax in zip(mDMs, axes):
    fluxes.mDM = mDM
    ax.set_title(rf"m$_{{\mathrm{{DM}}}}$ = {mDM}")
    ax.set_yscale("log")
    ax.set_ylabel("dN/dE")

    for channel in ["tau", "mu", "b", "Z"]:
        fluxes = PrimaryFlux(mDM=mDM, channel=channel)
        fluxes.channel = channel
        fluxes.plot(
            energy_bounds=[mDM / 100, mDM],
            ax=ax,
            label=channel,
            yunits=u.Unit("1/GeV"),
        )

axes[0].legend()
plt.subplots_adjust(hspace=0.9)
plt.show()

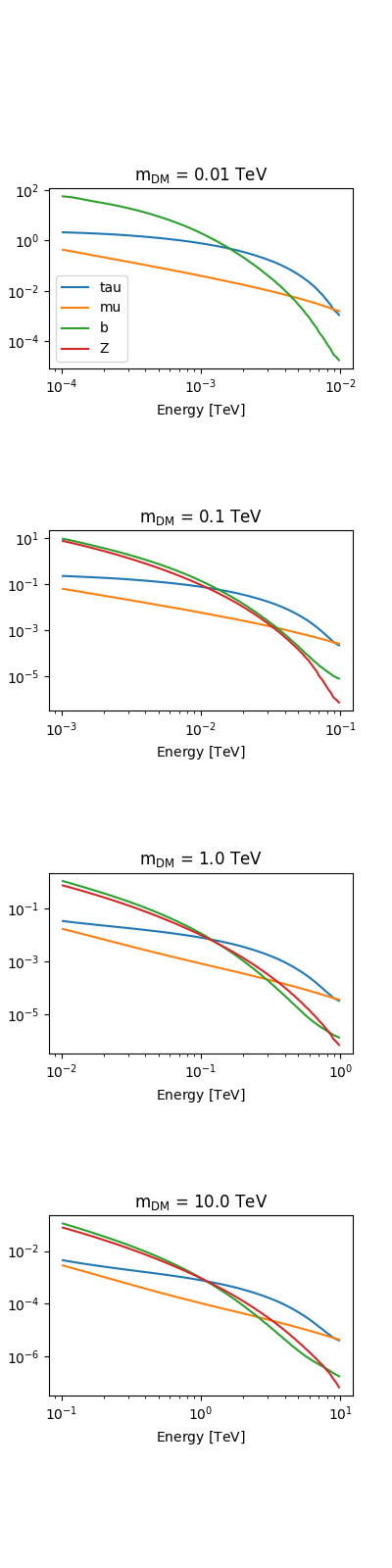
['eL', 'eR', 'e', 'muL', 'muR', 'mu', 'tauL', 'tauR', 'tau', 'q', 'c', 'b', 't', 'WL', 'WT', 'W', 'ZL', 'ZT', 'Z', 'g', 'gamma', 'h', 'nu_e', 'nu_mu', 'nu_tau', 'V->e', 'V->mu', 'V->tau']

Flux maps for annihilation

Finally flux maps can be produced like this:

channel = "Z"
massDM = 10 * u.TeV
diff_flux = DarkMatterAnnihilationSpectralModel(mass=massDM, channel=channel)
int_flux = (
    jfact * diff_flux.integral(energy_min=0.1 * u.TeV, energy_max=10 * u.TeV)
).to("cm-2 s-1")

flux_map = WcsNDMap(geom=geom, data=int_flux.value, unit="cm-2 s-1")
plt.figure()
ax = flux_map.plot(cmap="viridis", norm=LogNorm(), add_cbar=True)
plt.title(
    f"Flux [{int_flux.unit}]\n m$_{{DM}}$={fluxes.mDM.to('TeV')}, channel={fluxes.channel}"
)

plt.show()

Flux maps for decay

Finally flux maps for decay can be produced like this:

channel = "Z"
massDM = 10 * u.TeV
diff_flux = DarkMatterDecaySpectralModel(mass=massDM, channel=channel)
int_flux = (
    jfact_decay * diff_flux.integral(energy_min=0.1 * u.TeV, energy_max=10 * u.TeV)
).to("cm-2 s-1")

flux_map = WcsNDMap(geom=geom, data=int_flux.value, unit="cm-2 s-1")
plt.figure()
ax = flux_map.plot(cmap="viridis", norm=LogNorm(), add_cbar=True)
plt.title(
    f"Flux [{int_flux.unit}]\n m$_{{DM}}$={fluxes.mDM.to('TeV')}, channel={fluxes.channel}"
)

plt.show()